서 론
건물 에너지 분석은 주로 건물의 물리적 모델을 기반으로 에너지 부하를 분석하는 방향으로 진행되었다. 하지만 물리적 모델 기반 분석은 건물에 대한 자세한 지식이 요구되며 정확한 입력값이 제공되지 않으면 오류가 발생하거나 분석의 정확도가 저하될 수 있다(Amasyali and El-Gohary, 2018). 반면, 데이터 기반 분석은 시뮬레이션을 위해 건물에 대한 자세한 데이터가 필요하지 않고 과거 데이터로부터 학습한다. 이러한 장점으로 인해 발생 가능한 한계점이 다수 있음에도 불구하고 데이터 기반 건물 에너지 분석에 대한 다양한 선행 연구가 수행되었다(Wei et al., 2018).
데이터 기반 건물 에너지 분석은 데이터 양이 다양하고 많을수록 분석의 정확도가 상승하기 때문에 방대한 양의 데이터가 필요하다(Mathew et al., 2015). 따라서 공공데이터를 건물 에너지 분석에 활용하는 연구가 시도되었다(Cho and Yoo, 2021). 공공데이터를 기반으로 탄소 배출량이 높은 건축물의 사전진단이 가능해지면, 상세조사 대상건축물을 사전에 선별하여 현장방문조사에 소요되는 비용과 시간을 절약하는 등 다양한 정책적 이점이 발생할 수 있다.
이러한 사전 선별에는 ASHRAE Change point model (Kissock et al., 2003)이 활용될 수 있는데, 외기온도와 건축물 에너지 소비량의 상관관계 분석에 활용되는 모델이다. Change point model은 위 Figure 1과 같이 온도와 에너지 소비량의 연관성을 선형회귀 방식으로 분석하여 에너지 소비 패턴을 냉방에너지, 난방에너지와 기저에너지의 세 가지로 분리한다(Yoon, 2017). 물리적 모델 기반 에너지 시뮬레이션이 다량의 정보입력을 요구하는 데 반해, 에너지 소비량 데이터, 외기온도, 바닥면적과 같은 기본적 데이터만으로 건축물의 에너지 소비 특성을 간단히 분석할 수 있다는 장점이 있어, 다양한 영역에서 활용되고 있다(Jeong et al., 2021).
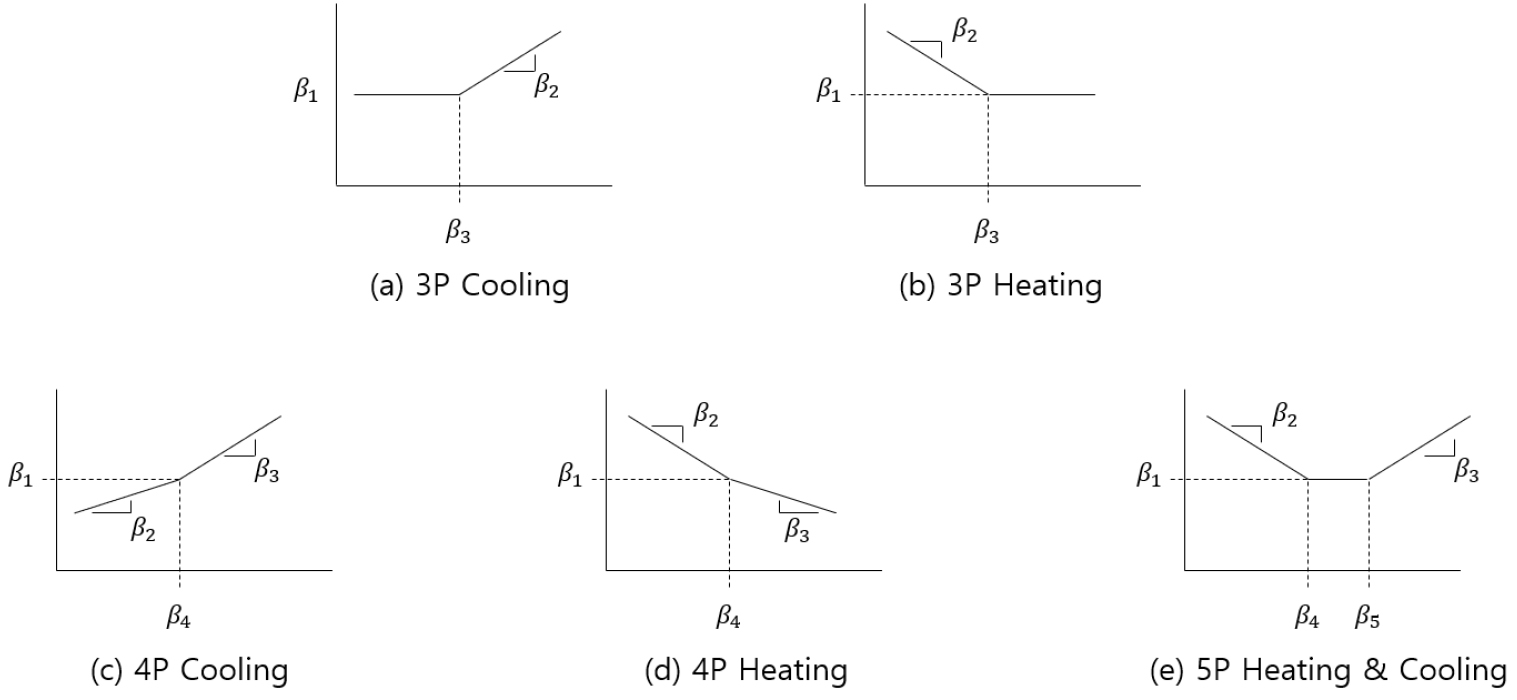
구체적으로는, 아래 Figure 2와 같이 외기온도에 따른 에너지 소비량의 분포에 따라 모델을 설정하고, 모델의 형상에 따라 구간별로 선형회귀계수를 계산하여 변화점(change point)과 냉난방 경사도로 건축물의 에너지 소비 특성을 표현한다. 도출된 회귀식의 결과에 따라 모델의 종류가 변화하며, 기저사용량 구간의 변화가 없고 냉방 사용량만 존재하는 3P Cooling 모델, 동일하게 기저사용량 구간의 변화가 없으나 난방 사용량만 존재하는 3P Heating 모델, 기저사용량 구간의 경사가 존재하고 냉방 사용량만 존재하는 4P Cooling 모델, 기저사용량 구간의 경사가 존재하고 난방 사용량만 존재하는 4P Heating모델과 기저사용량, 냉방 사용량 및 난방 사용량이 모두 존재하는 5P 모델이 존재한다. 이 중 4P 모델의 경우, Kissock et al. (2003)의 선행 연구에서 그림에 표현되지 않았으나, V자 형상을 띠는 4P Heating & Cooling의 결과 또한 존재한다.
CPM의 회귀 계수를 도출하는 방법론은 다양하다. 해당 모델이 제안된 Kissock의 연구에서는 Two part Grid-search 방법론이 가장 최적인 것으로 제시되었으나, 2018년에 수행된 미국 에너지부(Department of Energy: DOE)와 버클리 국립연구실에 의해 수행된 연구(Li et al., 2019)에서는 최소자승법이 사용되었으며, Jeong et al. (2021)의 연구에서는 Grid-search 방법론을 개선한 Modified Grid-search Method가 제시되었다. 본 연구에서는 공공데이터 기반의 건물 에너지 진단을 목적으로 하므로, 가장 유사한 환경조건을 갖는 DOE의 최소자승법 방법론을 사용하였다.
일반적으로 데이터 기반 모델에서 데이터 해상도는 모델의 정확도에 영향을 미치며(Jain et al., 2014; Kim et al., 2022), 이에 대한 다양한 선행 연구가 수행되었다. Choi et al. (2015)은 월간, 일간, 시간당의 다양한 외기온도 데이터를 적용하여 난방기, 냉방기, 중간기의 3개 구간으로 나누어 건축물의 선형회귀분석을 수행하였으며, Jung (2021) 또한 시간단위로 계측된 건축물의 에너지사용량에 대해 하절기, 동절기의 2개 구간으로 나뉜 V자 형태의 change point가 고정된 모형을 구축하고, 외기온도의 최적 데이터 해상도를 찾는 연구를 수행하였다. 그러나 선행 연구들은 고정된 change point를 기반으로 회귀 계수 도출을 수행하는 모델을 기반으로 데이터 해상도를 비교하였으며, 데이터에 따라 change point가 변화하는 모델을 기반으로 데이터 해상도를 비교한 연구는 아직 수행되지 않았다.
따라서 본 논문은 동적 change point가 반영되는 change point model의 데이터의 시간해상도에 따른 변화를 알아보고, 최적의 데이터 해상도를 도출하고자 한다. 구체적으로는 대상 건축물에 대해 수집된 데이터의 냉방, 난방 에너지사용량을 통해 change point의 참값을 확인하고, 전체 에너지사용량의 데이터 시간해상도를 바꾸어 가며, change point model을 적용한 뒤, 가장 참값과 가까운 change point가 도출되는 시간해상도를 탐색하고자 한다.
시뮬레이션 개요
대상 건축물 특성 및 데이터 처리 과정
전력으로 냉난방을 수행하는 일반 업무시설 건축물을 대상으로 선정하였으며, 해당 건축물의 세부 정보는 아래 Table 1과 같다.
Table 1.
Characteristics of the building
대상 건축물의 2017년 1년간 계측된 데이터를 사용하였다. 수집된 데이터는 냉방 및 난방 사용량이 각각 구분되어 있으며, 전체적인 데이터 획득부터 결과 도출까지의 프로세스는 아래 Figure 3과 같다. 획득된 데이터의 전처리(preprocessing) 과정을 거치고, 전처리 과정은 결측치 탐지(missing value detection)와 이상치 탐지(anomaly detection) 과정으로 나뉘어진다. 데이터의 리샘플링 또한 일반적으로는 전처리 과정에 포함되나, 본 논문에서는 데이터의 시간 간격을 변화시키며 차이를 보고자 하기 때문에, Change point model의 연산마다 매 번 시간 간격을 바꾸어 리샘플링이 반복되므로, Change point model 알고리즘의 연산(processing) 과정에 포함시켰다. 사용량에 대한 데이터를 다루므로, 리샘플링 과정은 지정된 시간 간격에 따라 각 구간의 사용량을 적분하여 해당 간격의 값으로 취한다. 전처리가 마무리 된 뒤에는 1시간, 2시간, 3시간, 6시간, 12시간, 1일, 2일, 3일, 1주, 2주, 1개월의 총 11가지의 값으로 데이터의 시간 간격을 변화시키며 재실시간 필터링을 거치고, Change point model의 결과값을 도출한다. 11번의 시행이 끝난 뒤, 결과값을 취합해 비교하여 최적의 시간 해상도가 도출된다.
상세한 데이터 처리 및 최적 시간해상도의 비교 방안은 아래 Figure 4와 같다. 냉방, 난방의 사용량이 분리 계측되었으므로, 해당 데이터를 분리해서 일 단위로 리샘플링을 수행한 뒤 Change point model 프로세스를 처리할 경우 3P model이 각각 2개 도출된다. 해당 결과를 기반으로 대상 건축물의 냉방 시작온도와 난방 시작온도를 확인할 수 있으며, 이를 change point의 참값(True change point)이라고 간주한다. 그리고 냉방, 난방 및 기저에 해당되는 기타 전력 사용량을 합한 총 사용량(total consumption)을 별도로 합산하여 마찬가지로 리샘플링을 수행하되, 앞서 설명된 11가지의 각기 다른 시간 간격으로 수행한다. 이후, 개별 리샘플링 데이터를 재실시간 처리 프로세스와 Change point model 프로세스에 통과시켜 개별 시간해상도의 change point가 얻어지게 된다. 얻어진 값은 개별 해상도 데이터를 사용하여 예측된 CP (Estimated CP)가 되며, 이 값과 참값과의 차는 예측 CP의 오류(Error)가 된다. 가장 오류가 낮은 시간 해상도를 확인하면 가장 참값과 가까운 CP를 예측하는 시간 해상도를 알 수 있고, 이를 최적 해상도로 결론지을 수 있다.
재실시간 처리 프로세스는 냉방 및 난방이 가동되는 재실시간만을 고려하기 위한 것으로, 데이터에서 비 재실 시간을 제외한다. 월 단위 및 주 단위의 경우는 별도의 고려가 불가능하므로 처리가 이루어지지 않으며, 일 단위의 경우는 공공데이터포털을 통해 한국천문연구원에서 제공하는 특일 정보제공 API를 통해 국경일 정보를 받고, 국경일과 주말이 아닌 값만을 취한다. 시간 단위의 경우는 앞선 일별 처리절차와 함께 재실 시간구간 또한 고려한다. 재실 시간구간은 표준 근로시간인 09시부터 18시까지로 설정되었으며, 2, 3시간 등 복수의 시간단위의 경우는 리샘플링이 이루어진 이후의 값을 기준으로 데이터 타임스탬프의 재실 시간구간 포함 여부를 고려하였다.
원 데이터가 시간 단위 데이터이므로 재실 시간구간만을 전부 추출한 뒤 리샘플링을 수행하는 것 또한 가능하지만, 실제 공급되는 데이터의 경우 이러한 고려가 불가능하다. 대표적으로 공공데이터포털에서 제공되는 월 단위의 건물에너지사용량 데이터의 경우, 재실 시간구간이 아닌 월 전체의 데이터를 제공한다. 본 논문은 향후 리샘플링된 데이터가 아닌 외부에서 공급되는 데이터의 활용을 실질적인 측면에서 반영하고자 하였으므로, 획득 이후의 리샘플링 과정만을 모사하였다.
결과 및 토의
데이터 처리 결과
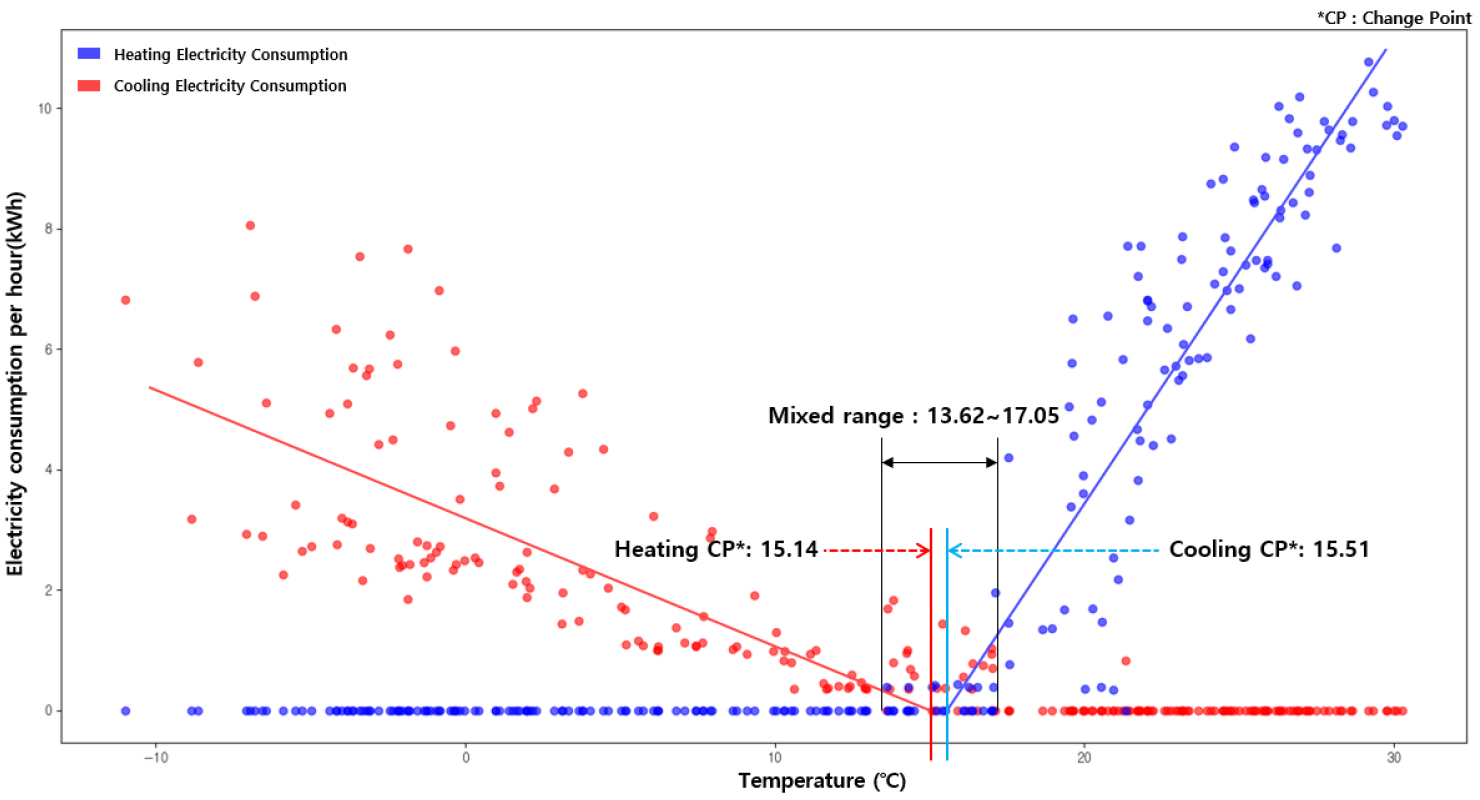
우선 분리된 일 단위의 냉방 및 난방 사용량으로 change point의 참값을 도출하였다. 도출된 참값은 난방의 change point (heating change point)가 15.14℃, 냉방의 change point (cooling change point)가 15.51℃ 였으며, 분리된 사용량 기반의 change point model의 처리결과 및 데이터 포인트는 아래 Figure 5와 같았다. 데이터 포인트를 통해서 13.62℃부터 17.05℃ 구간에 냉방 및 난방 사용이 동시에 존재하는 것이 확인되었다.
이후 합산된 총 사용량에 대하여 시간 간격을 바꾸어 가며 change point model 프로세스를 수행하였다. 도출된 결과는 아래 Table 2, Table 3과 같았다. Table 2는 비교하고자 하는 change point값, change point model의 종류와 모델의 에너지 사용량 예측에 대한 평균 제곱근 편차(root mean square error: RMSE)를 나타내며, Table 3은 change point model로부터 도출되는 건축물의 특성인 난방경사(heating slope), 냉방경사(cooling slope), 기저사용량(base consumption), 난방사용량(heating consumption), 냉방사용량(cooling consumption)을 보여 준다.
Table 2.
Estimation result of CP model along different time interval
Table 3.
Result of slope, consumption along different time interval
결과 분석
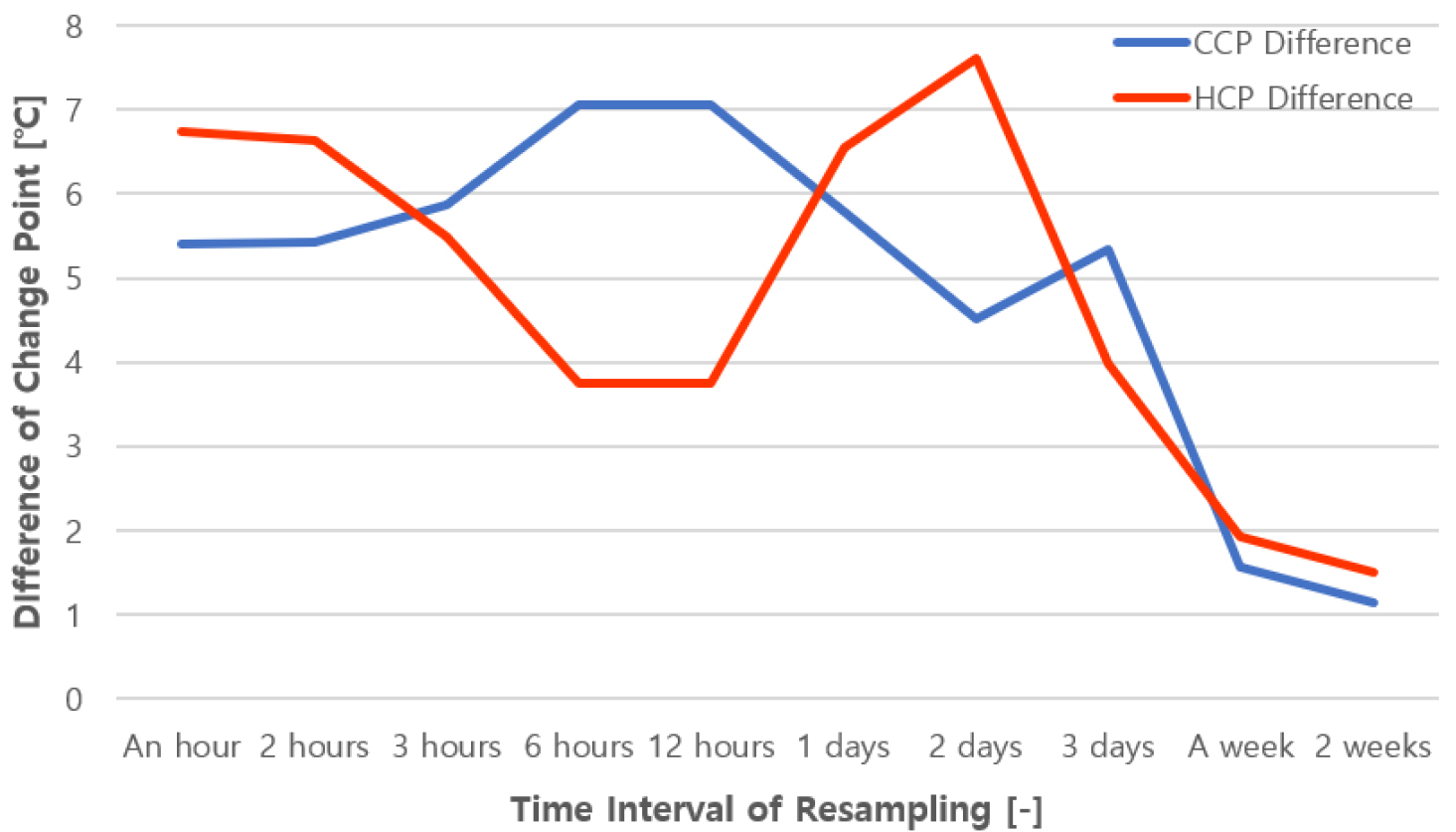
시간 간격에 따른 예측 CP와 CP의 참값의 차는 아래 Figure 6과 같이 나타났다. 시간 단위와 1일 간격에서는 5℃ 정도의 오차가 유지되었고, 그 이상의 시간 간격이 될수록 차이가 감소하여 2주의 시간 간격에서 가장 낮은 예측 CP의 오차가 도출되었다. 해당 결과에 따르면 CP를 예측하기 위한 최적의 시간 간격은 2주이다. 또한, 0.36℃의 차이가 있으나, Figure 5에서 드러난 냉방 및 난방의 형상은 4P 모델에 가까워, 모델의 형상에 대한 예측 자체도 1주, 2주의 간격을 갖는 데이터가 더 유사한 것으로 나타났다.
Table 2에서 냉방의 change point는 시간 간격에 따른 경향성은 없으나, 1주 단위 이상 간격에서 크게 변화하는 모습을 보였으나, 참값이 15.51℃ 였으므로, 오히려 더 참값에 가까워진다는 결론이 도출되었다. 난방의 change point 또한 유사하게 짧은 시간 간격에서는 8.4℃ ~ 11.4℃ 의 범위에 분포하였으나, 1주 단위 이상이 될 경우 16℃ ~ 17℃로 크게 상승하였다. 이 경우 또한 참값이 15.14℃ 였으므로, 더 가까워진다. 따라서 2주 간격이 가장 적합하다고 볼 수 있으나, 모델의 RMSE값은 데이터의 시간 간격이 짧아질수록 감소하는 추세를 보였다.
위 Figure 7과 같이 일 단위로 리샘플링된 데이터의 결과를 보았을 때, 이는 기저 사용량으로 처리되는 냉, 난방 이외의 전기사용량 및 건축물의 사용 패턴과 연관이 있는 것으로 보인다. 분리된 냉방 사용량 및 난방 사용량을 표현하는 Figure 5의 데이터포인트와는 달리, 냉방구간의 데이터포인트의 분리가 뚜렷하게 이루어지는 경향이 확인되었다. 난방구간에서도 일부 분리되는 모습이 확인되었으나, 포인트의 수가 많지 않아 정상적으로 change point model 회귀식의 fitting이 이루어진 반면, 냉방구간에서는 절반 정도의 비율로 분리되었으므로, segmented regression 과정에서 가장 RMSE가 낮아지는 중앙 직선으로 수렴해 해당 구간이 전부 기저 구간으로 처리된 것으로 추정된다. 이는 1일 간격의 데이터에서 도출된 특이한 수치의 원인을 설명한다.
이러한 분리는 주로 건축물이 사용되지 않는 주말 및 공휴일이 데이터에 포함되어 있을 경우 발생하는데, 공휴일 및 주말은 전처리 과정에서 이미 제외되었으므로, 대상 건축물이 평일 중 사용되지 않는 날의 비중이 높을 수 있다고 가정할 수 있다. 그러나, 이 경우 업무시설에서 사용되는 기기 전력이나 조명 전력이 동일하게 비사용 상태가 되므로 기저 사용량까지 낮아지는 형상이 나타나야 하나, 해당 사례에서는 그러한 형상이 관측되지 않았다. 이에 대해 고찰한 결과, 개별 난방기구가 사용되기 때문으로 추정하였다. 대상 건물은 중앙공조가 이루어지는 건물로, Figure 5에서 표현된 냉방 및 난방 사용량은 중앙공조시스템의 냉방 및 난방 사용량이다. 그러나 콘센트에 연결하여 사용하는 전열기계, 선풍기 및 냉풍기와 같은 개별 냉방 및 난방기구는 냉방 및 난방을 수행함에도 불구하고 기기 전력사용량으로 취급되기 때문에, 위 Figure 5와 같은 냉방 및 난방전력만 표시하였을 때에는 반영될 수 없다. 이를 통해 Figure 5과는 다르게 Figure 7에서 난방 구간의 사용량이 더 높은 모습을 보이는 현상 또한 설명이 가능하다.
따라서 이를 전부 고려하였을 때, 대상 건축물은 하절기의 절반 정도를 중앙냉방을 가동하지 않거나 적게 가동하고, 개별 냉방기기만 사용하고 있으며, 개별 난방기기의 사용량 또한 높다는 결론을 내릴 수 있다. 또한, 참값으로 사용된 냉방 사용량 및 난방 사용량이 중앙 공조의 사용량만을 반영하고, 개별적으로 사용되는 전열 기기와 같은 개별 냉난방 사용을 반영하지 못하는 부분에 대한 한계점 또한 존재한다고 할 수 있다.
마지막으로, 해당 건축물의 경우 월별 데이터는 모델이 도출되지 않았으며, 1년치의 월별 데이터로는 회귀식의 fitting이 불가능했다. 이는 공공데이터 기반의 건축물 선별 절차의 수립을 위해서 공공데이터에서 일정 수준의 해상도 증가가 필요함을 사사한다.
한계점
본 논문은 동적 변화가 존재하는 change point model을 대상으로 데이터 간격에 따른 모델의 변화를 연구하였다. 참값과 가장 유사한 데이터 간격을 도출하였으나, 몇몇 한계점이 존재한다.
첫째는 데이터 모수에 따른 한계점이다. 대상건물에 대해 수집된 2017~2021년도의 총 5개년도 데이터가 존재하나, 본 연구는 2017년도의 1개년도 데이터만을 다루었으며, 1개 건축물만을 대상으로 수행되었다. 2019년도 이후의 데이터는 COVID-19의 영향으로 인해 배제되었으며, 2018년도의 데이터는 데이터 전처리 과정에서 결측치 및 이상치가 많아 사용이 불가능했다. 향후 최신 데이터 수집을 수행하고, COVID-19의 영향도를 선행연구 고찰을 통해 반영하여 후속 연구를 진행하고자 한다.
둘째는 대상건물의 명확한 속성 반영이다. 일반적인 사무용도 건물과는 다른 사용 패턴이 분석을 통해 탐지되었으며, 이는 건축물의 주 용도만으로 재실시간을 구분할 수 없음을 시사한다. 향후 재실 시간을 별도로 측정하거나, 별도의 추정 알고리즘을 마련하여 표준 재실시간대가 아닌 실질적 재실시간을 반영하도록 개선할 것이다.
결 론
본 논문은 change point model 상의 데이터 시간해상도에 따른 영향을 조사하고, 최적의 데이터 해상도를 도출하였다. 수집된 데이터의 분리된 냉방 및 난방 사용량을 기준으로 change point model을 적용해 참값을 얻고, 전체 사용량을 기준으로 데이터의 시간 해상도를 바꾸어 리샘플링을 반복하며 change point model을 적용해 결과의 변화를 관측하고 최적의 시간 해상도를 도출하였다.
RMSE는 데이터의 시간 해상도가 정밀해질수록 감소하는 결과를 보였으나, 그럼에도 불구하고 도출된 최적의 시간 해상도는 2주였다. 이에 따른 원인을 분석한 결과, 높은 개별 냉방 및 난방기기의 사용이 원인으로 추정되었으며, 이는 change point model의 건축물 상 적용을 위해서는 개별 냉방 및 난방기기의 사용여부 및 빈도에 대한 고려가 중요함을 의미한다.
추가로, 1년치의 월별 데이터로는 지나치게 적은 모수로 인해 change point model이 도출되지 못했다. 이는 현재 제공되는 월 단위의 에너지사용량 공공데이터의 해상도로는 분석이 불가능함을 의미하고, 연간 편차를 무시하고 다년간 데이터를 사용해야 월 단위 데이터 기반의 분석이 가능함을 보인다. 그러므로, 보다 정확한 분석을 위해서는 공공데이터의 개선을 통해 데이터의 시간 해상도를 제고해야 할 것이다.
본 논문은 공공데이터 기반의 건축물 에너지 진단을 목적으로 데이터의 시간 해상도에 따른 영향을 조사하였고, 최적 해상도를 도출하는 프로세스를 제시하고 수행하였다는 점에 그 의의가 있다. 향후 더 많은 데이터를 수집하여 부족한 모수에서 오는 한계점을 개선함과 동시에, 공간 사용특성에 따른 개별 냉방 및 난방기기의 영향을 상세히 고려하여야 할 것이다. 구체적으로는, 재실패턴 및 기기사용전력 등에 대한 더욱 정밀한 데이터셋을 구축하여 개별 냉방 및 난방기기의 전체 사용량에 대한 영향도를 확인하여야 하며, 냉방 및 난방 사용량의 일부가 기기 사용량으로 나누어지는 현상이 관측되었으므로, 분리계측의 기준을 이에 맞추어 변경하기 위한 연구 또한 수행되어야 한다. 최종적으로는 총 사용량을 통한 change point model 기반의 건축물 에너지 진단을 위한 연구를 고도화하고자 한다.