서 론
최적전력운영 개요
수요-분산자원 자료특성
국내 전력요금제도
최적화 기법
마이크로그리드 전력최적운영 전략
최적화 기법 성능비교
시간별 최적화 성능
최적화 기법별 경제성 분석
분산자원 요금할인제도 기반 운영비용 개선안
최적 기법 선정
결 론
서 론
최근 마이크로그리드(Micro-Grid)의 안정적인 운영 및 관리를 위해 효율적인 수요-분산자원 연계운영의 중요성이 증가하고 있다(Kim, 2014). 정부는 태양광(PV, photovoltaics), 풍력(WT, windturbine) 등 신재생에너지원의 할인요금제도 등의 정책을 수립을 통해 수요-분산자원을 연계한 전력운영을 활성화시키고 있으나, 신재생에너지원의 지리적, 기상적 요인 등에 의한 불안정한 출력특성으로 인해 전력수급품질이 악화되고 있다. 이러한 신재생에너지원의 간헐적인 출력을 보완하기 위해 에너지저장장치시스템(ESS, energy storage system)을 활용한 전력 수급균형 유지에 대한 노력이 확대되고 있으며, 다양한 수치적 모델, 최적화 기법을 활용한 마이크로그리드 구성요소의 최적설계와 이를 연계한 전력운영 최적화에 대한 연구가 수행되고 있다.
국내의 마이크로그리드 구성요소 최적설계에 관한 연구로 Na and Kim (2019)는 확률적 기법(COPT, Capacity Outage Probability Table)을 이용하여 전력손실을 고려한 풍력 및 태양광 발전 시스템의 최적 용량 및 위치를 제안하였다. Lee et al. (2018)은 신재생에너지 뿐만 아니라 경제성을 고려한 태양광발전시스템 연계형 에너지저장장치의 최적 설계 용량을 제안하였으며 태양광 발전시스템의 용량(100 kW 기준) 대비 평균 2.88배의 용량(288 kW)이 산정되었다. 마이크로그리드 내 구성요소의 설계 최적화뿐만 아니라 분산-수요자원을 연계한 최적전력운영에 대한 연구도 이루어지고 있다. Chang and Kang (2017)은 마이크로그리드 내 전력소비량 및 신재생에너지원의 예측을 고려한 국내 전력요금제 기반으로 분산형 전원(PV, ESS)의 최적제어 및 운영 기법을 제시하였다.
국외의 경우 다양한 마이크로그리드 구성요소의 최적설계, 그리드 운전 최적화 및 전력요금제 기반의 경제성 분석까지 이루어지고 있다. Cen et al. (2018)은 실제 마이크로그리드 내 분산자원(PV, ESS)을 활용하여 각 분산자원의 시간별 최적운영 스케줄을 수립하였으며 이를 통한 전력에너지 성능을 평가하였다. Banaei and Rezaee (2018)은 시뮬레이션 데이터를 활용하여 마이크로그리드 내 다양한 분산자원(PV, WT, 그리고 ESS)의 최적용량설계와 Fuzzy기법을 기반으로 3단계의 전력운영비용 최적화 모델을 개발을 통해 전력 에너지 및 비용을 분석하였다.
국내외적으로 개별 최적화 기법을 활용한 다양한 마이크로그리드 구성요소의 최적설계, 전력요금제 기반의 마이크로그리드 운전 최적화 및 경제성 분석에 대한 연구는 이루어지고 있으나 그리드 설계단계에서 다양한 최적화 기법의 성능비교를 통한 적정한 기법 선정이 선행되어야 할 필요가 있다.
이에 본 연구에서는 초소형 마이크로그리드를 대상으로 세 가지 메타 휴리스틱 기법(Mixed-integer Linear Programming, Genetic Algorithm, Pattern Search)의 성능 비교분석을 통한 그리드의 시간별 최적 전력운영 기법을 제시하고, 선정된 최적화 기법을 활용한 국내 분산자원 요금할인제도 기반의 운영비용 절감 개선안을 제시하고자 한다.
최적전력운영 개요
수요-분산자원 자료특성
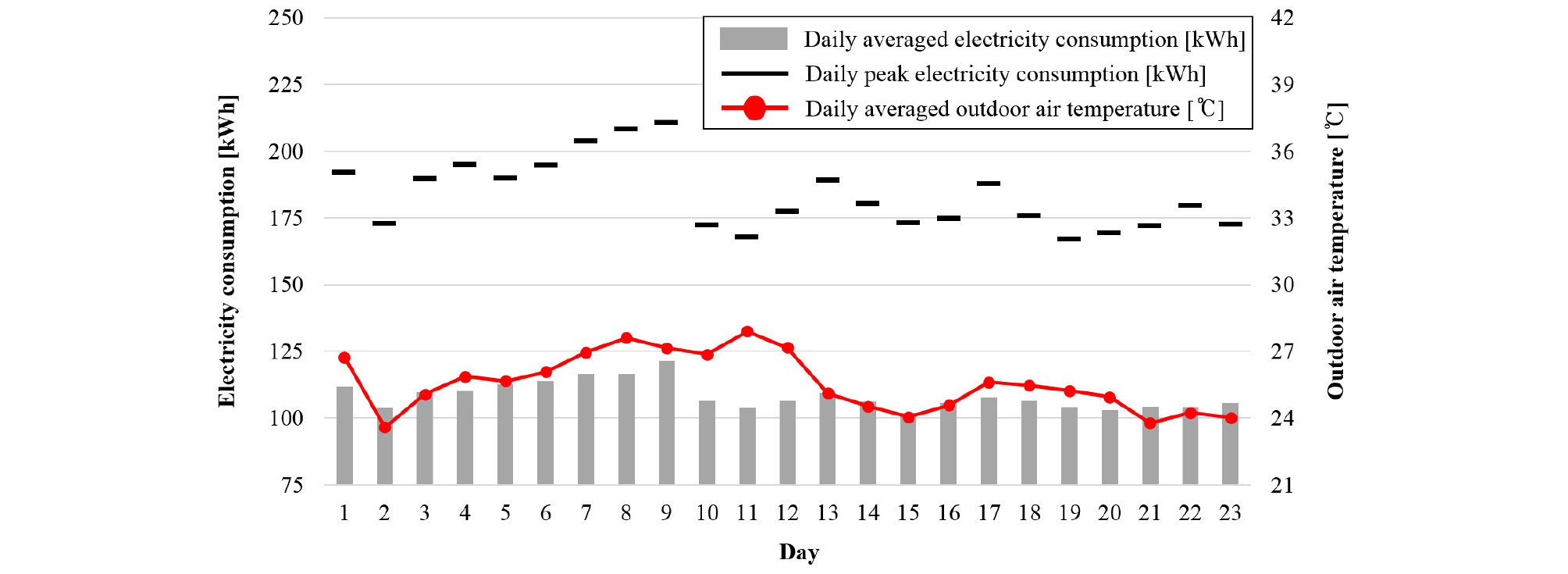
미국 EIA (Energy Information Administration)는 4년 주기로 CBECS (Commercial Buildings Energy Consumption Survey)를 실시하고 있으며 5백만 개 이상의 상업용 건물을 대상으로 건물 특성 및 에너지 사용량의 정보를 제공하고 있다(EIA, 2015). 본 연구에서는 CBECS를 기반으로 초소형 마이크로그리드를 구현하기 위해 미국 중소형 규모의 표준형 상업용 건물을 선정하였으며, 건물 위치는 인천지역으로 가정하였다. 대상건물은 연면적 4,982 ㎡의 지상 1층/지상 3층 규모로 건물 내 HVAC 시스템은 VAV시스템으로 설정하였다. 재실 및 HVAC 스케줄, 조명/재실부하는 ASHRAE (American Society of Heating, Refrigerating, and Air conditioning Engineers) Standard 90.1 기준(ASHRAE, 2016)에 근거하여 설정하였으며, 이외 건물의 특성은 Table 1과 같다. 앞서 구성된 건물을 대상으로 연구기간을 선정하기 위해 사전에 월별 전력소비량의 비교분석을 수행하였으며 하절기 중 8월의 평균 전력소비량(주중 기준)이 64,198 kWh로 가장 높았다. Figure 1은 대상건물의 월별 전력소비량이 가장 높은 8월의 일별 평균 전력소비량 및 최대 전력소비량(주중 기준)을 나타낸 것으로 일별 평균 전력소비량과 일별 최대 전력소비량은 유사한 특성이 나타났으며 외기온도와도 유사한 경향을 나타냈다. 이에 세 가지 최적화 기법의 성능비교 기간은 8월 내 일별 평균 전력소비량과 일별 최대 전력소비량이 가장 높은 day 9(최대 부하일)를 적용하였으며 경제성 분석 시 1개월 간 전력소비량 정보 및 분산자원 정보를 활용하였다.
Table 1. Set conditions for commercial building based on CBECS
Table 2는 대상건물에 연계되는 분산자원(PV, ESS)의 정보를 나타낸 것으로 각 분산자원은 건물의 전력소비 규모와 분산자원 설치비용, 그리고 기존 분산자원 최적용량 산정연구(Lee et al., 2018)를 고려하여 PV (50 kW), ESS (100 kW)로 선정하였다. 각 분산자원의 기본적인 운영의 경우 PV는 가장 맑은 날의 생산량을 기준으로 순시활용, ESS는 수명을 고려한 잔존 용량구간(SOC, State of Charge) 및 순간 충/방전 비율을 적용하여 시간별 ESS 충/방전 스케줄에 따른 각 최적화 기법별 마이크로그리드의 최적 전력운영 스케줄을 수립하였다.
Table 2. Characteristics for PV generation system and ESS
국내 전력요금제도
국내 전력요금은 기본적으로 기본요금, 전력량요금으로 구성되며 각 건물용도에 따라 계시별 차등요금제(TOU, Time-of-Use)가 적용되고 있다. 그 중 산업용, 일반용, 그리고 교육용 건물에 대해서는 선택요금제를 통해 소비자의 전력특성을 반영하고 있다. Table 3은 국내 일반용 건물의 전력요금표(일반용 전력(갑)Ⅱ-고압A)를 나타낸 것으로 대상건물은 계약전력 300 kW 미만(180 kW)으로 일반용 전력(갑) 전기요금에 해당되며 본 연구에서는 하절기 내 시간별 소비량 절감에 유리한 ‘고압A-선택Ⅱ’ 요금제를 선정하였다.
Table 3. TOU electricity price system in summer season for commercial building
산업통상자원부와 한국전력공사(산업통상자원부, 2017)는 2017년 5월부터 2020년까지 ‘친환경 투자 전기요금 할인특례 제도’를 통해 신재생에너지 및 ESS를 설치하고 일반용·산업용 전기를 사용하는 고객을 대상으로 분산자원의 보급 확대 및 활성화를 가속화하고 있다. Table 4는 신재생에너지(PV) 와 ESS를 연계할 경우 요금할인특성을 나타낸 것이다. 먼저, PV는 자가소비로 가정할 경우 신재생에너지 할인금액(발전량(kWh)*전력판매단가(150원/kWh))의 50%의 추가 할인혜택 대상이며 상기 할인금액에 20% 추가 할인이 가능하다. ESS를 적용할 경우 기본적으로 경부하 구간의 전력량 요금에 대해 50% 할인, 최대부하 구간에 전력소비 감소를 통해 3배의 기본요금 할인혜택을 적용할 수 있으며 ESS 비중이 계약전력 대비 10% 이상으로 상기 전력 할인금액에 1.2배의 추가할인이 가능하다. 상기 요금할인특성은 주로 경부하 구간의 ESS 충전, 최대부하 구간의 ESS 최대방전을 통한 전력운영 비용절감전략이 유리한 조건으로 구성되어 있어 본 연구에서는 분산자원을 통한 최대부하 절감전략(Peak-cut mode)을 바탕으로 시간별 전력운영 스케줄을 구성하였다.
Table 4. Discounted price system of distributed energy resources
최적화 기법
초소형 마이크로그리드의 전력운영비용 최소화를 목적으로 최적화 기법을 적용하기 위해 세 가지 메타 휴리스틱 기법(MOAs, Meta-heuristic Optimization Algorithms)을 적용하였다. 메타 휴리스틱 기법은 특정문제에 구속되지 않고 여러 복잡한 조건에서 최적해 탐색성능이 뛰어나며 Mixed-integer Linear Programming (MILP), Pattern Search (PS), Genetic Algorithm (GA), Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO), Simulate Annealing (SA), Cross-Entropy (CE) 등의 다양한 기법이 여러 분야에서 적용되고 있다(Shaheen et al., 2018). 이에 본 연구에서는 다양한 메타 휴리스틱 기법 중 최적해 탐색방법이 각기 다른 MILP, GA, 그리고 PS의 세 가지 메타휴리스틱 기법을 활용한 마이크로그리드 운영전략을 비교분석하였다.
MILP 기법은 의사결정변수를 기반으로 여러 선형 제한조건을 충족하면서 가변 요소 사이에 일차 방정식이 성립될 경우 실수해/정수해의 최적해를 탐색하며 최적화 속도가 빠르고 효율이 높다(Lotero et al., 2016). MILP 기법과 달리 GA기법은 생물의 진화과정을 기반으로 세대(generation)를 증가시키면서 진화과정을 되풀이한다. 이 경험적인 최적해 탐색 과정을 통해 비교적 학습회수 및 소요시간이 많은 특성이 나타난다(Qiu et al., 2015). 마지막으로 PS는 초기점(initial point)를 중심으로 주어진 제한 조건에서 격자간격(mesh)을 따라 패턴을 반복하며 최적해를 찾아가는 기법이다. 특정 공간상에서 최적해를 탐색함으로써 결과해석이 용이하며 비연속적이고 미분이 어려운 문제해결에 용이하다(Sahu et al., 2015).
Table 5는 세 가지 메타 휴리스틱 기법에 공통적으로 적용한 의사결정변수, 목적함수, 제한조건 및 경계조건을 나타낸 것이다. 기본적으로 각 기법은 의사결정변수를 기반으로 제한조건, 경계조건 내 최적해를 탐색한다. 본 연구에서는 주로 ESS의 충/방전 스케줄에 따른 전력을 구성하여 의사결정변수는 ESS의 비가동/가동 여부를 나타낸다. 제한조건은 크게 최소소비량이 0 이상, ESS의 잔존용량(전 구간)과 해당 구간의 ESS 충/방전 스케줄의 합은 ESS의 잔존용량(해당 구간)으로 구성되어 있다. 경제조건의 경우 ESS의 최대/최소 순간 충/방전량, ESS의 최대/최소 잔존용량(해당 구간)으로 설정하였다. 상기 조건에 따라 각 기법을 구성하였으며 이에 따른 각 기법의 최적화 성능을 비교분석하였다.
Table 5. Set conditions for different three meta-heuristic optimization algorithms
마이크로그리드 전력최적운영 전략
수요-분산자원 연계형 마이크로그리드의 시간별 전력 최적 전력운영 스케줄을 수립하기 위해 세 가지 메타 휴리스틱 기법에 대해 정식화하였다. 공통적으로 다양한 제약조건 내 전력운영비용을 목적으로 구성하였으며 PV는 순시활용으로 주로 ESS의 충/방전 스케줄에 따른 전략을 식 (1)~(6)과 같이 수립하였다. 식 (1)은 의사결정변수로 ESS의 비가동(xt=0), 가동(xt=1)을 나타낸 것이고 식 (2)인 목적함수를 기준으로 식 (3)~(6)의 제약조건 내 각 부하구간별 전력소비량(Lt), PV생산량(PVt), 그리고 시간별 ESS 충/방전량(ESSt)으로 구성하여 최소비용(Pmin)이 도출된다. 식 (3)은 최소부하가 0 이상의 조건을 나타낸 것이며 식 (4)는 ESS의 시간별 잔존용량(SOCt)을 수식화한 것이다. 그리고 식 (5), (6)은 각각 ESSt와 SOCt 의 범위를 나타낸 것이다.
| $$x_t=0,\;x_t=1$$ | (1) |
| $$f(P_\min)=57,4\ast{(L_t=PV_t+ESS_t)}_{off}+108.6\ast{(L_t=PV_t+ESS_t)}_{mid}+131.1\ast{(L_t=PV_t+ESS_t)}_{on}$$ | (2) |
| $$L_t=PV_t+ESS_t\;\geq\;0$$ | (3) |
| $$SOC_t=SOC_{t-1}+ESS_t$$ | (4) |
| $$-40kW\;\leq\;ESS_t\;\leq\;+40kW$$ | (5) |
| $$+10kW\;\leq\;SOC_t\;\leq\;+90kW$$ | (6) |
위 의사결정변수, 목적함수, 그리고 제약조건을 활용하여 세 가지 최적화 기법에 대한 시간별 전력운영 최적화 성능 비교분석 및 경제성을 평가하였다.
최적화 기법 성능비교
시간별 최적화 성능
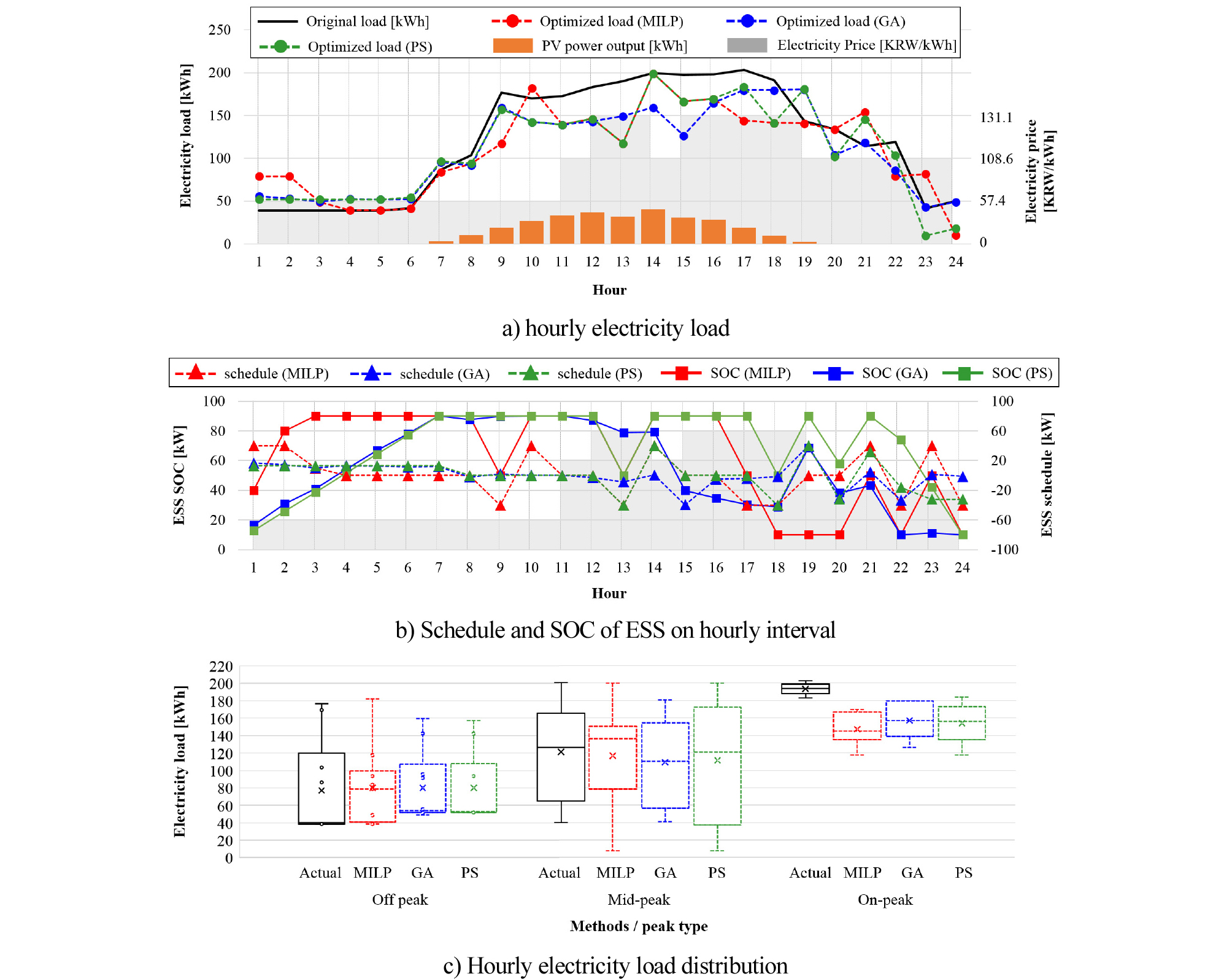
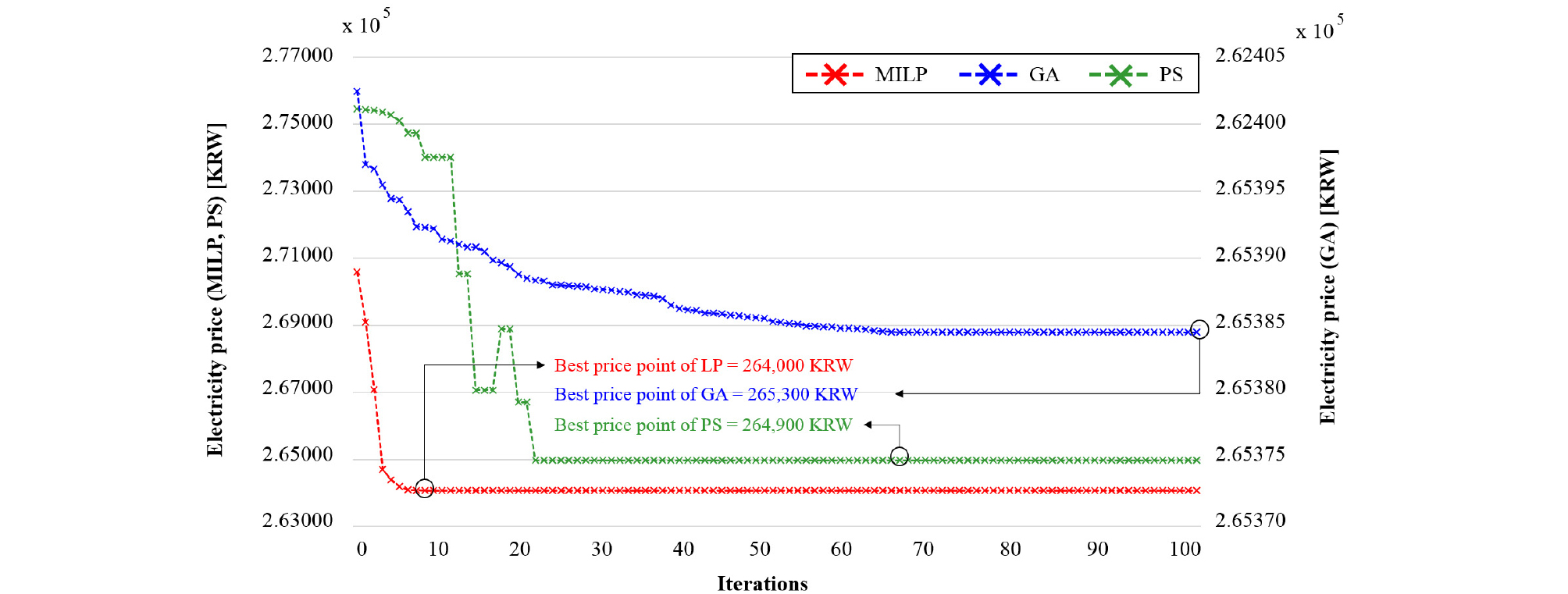
본 절에서는 TOU 전력요금을 기반으로 3가지 최적화 기법 간의 시간별 전력운영 최적성능 비교분석을 수행하였다. 기본적으로 전력요금은 기본요금 + 전력량요금으로 구성되어 있으나, 계시별 요금제에 따른 운영성능을 검토하기 위해 매시간별로 사용되는 전력량요금만을 비교하였다. Figure 2 는 세 가지 메타 휴리스틱 기법을 활용한 최적화 전/후 시간별 전력소비량, ESS 충/방전 특성, 그리고 각 부하구간별 부하분포를 나타낸 것이다. 먼저, 경부하 구간에 대해 공통적으로 ESS의 충전을 통해 중간부하 및 최대부하 구간을 대비하고 중간부하 구간에서는 ESS의 충/방전, 최대부하 구간은 ESS의 최대방전을 통해 부하를 감소시키는 특성이 나타났다. 특히, MILP는 다른 기법에 비해 중간부하 구간에서 시간별 ESS의 방전을 최소화하고 최대부하 구간에서 ESS의 최대방전을 통해 비용을 절감하는 특성이 나타났다. Figure 3과 Table 6은 각 최적화 기법의 학습회수별 비용 최적화 과정 및 성능을 나타낸 것으로 MILP 기법은 가장 짧은 시간에 최적해에 도달하는 동시에 0.205794초의 최적화 소요시간, 9번의 학습, 그리고 264,000원의 전력요금으로 다른 기법에 비해 효과적이었다. GA 기법은 Figure 3과 같이 최적화 초기점(Initial)에서의 비용은 낮으나 기법 특성상 최적해를 탐색하는데 가장 많은 시간이 소요되었다. PS 기법은 MILP 기법에 비해 학습회수 대비 소요시간이 짧은 특성을 나타냈으나 최적해 탐색성능은 다소 저하되었다.
Table 6. Performance evaluation for different optimization algorithms
최적화 기법별 경제성 분석
각기 다른 일별 전력소비량, PV 생산량에 따른 각 최적화 기법별 전력량 요금을 비교분석하기 위해 1개월 간 전력량 요금을 검토하였다. Table 7은 각 최적화 기법별 1개월 간(주중 23일)의 전력량 요금을 나타낸 것으로 최적화 기법 적용 시 분산자원을 연계하지 않은 기존 전력소비량(Original) 대비 평균 6,066 kWh (9.45%)의 에너지 절감이 가능하였으며, 평균 778천원(11.78%)의 비용을 절감할 수 있었다. 각 최적화 기법별 성능결과, 부하 측면에서 1개월 간 유사한 절감특성이 나타났으나 MILP기법은 운영비용 측면에서 다른 기법 대비 최대 93천원의 추가비용 절감효과가 나타났다. 이는 MILP 기법 적용 시 중간부하 구간의 ESS 방전을 최소화하고 최대부하 구간 내 ESS 최대방전 전략수립을 통해 비용절감에 효과적인 것으로 판단된다. 이후 MILP기법을 활용하여 분산자원의 요금할인제도 기반의 전력운영비용 절감 개선안을 제시하고자 한다.
Table 7. Optimized electricity load and price with different optimization methods for 23 days in August
분산자원 요금할인제도 기반 운영비용 개선안
최적 기법 선정
본 절에서는 선정된 MILP 기법을 기반으로 분산자원의 할인요금제도 적용 시 1개월 간 마이크로그리드 운영 전체 전력요금(기본요금+전력량요금)을 평가하였다. 식 (7)은 앞서 정의한 Table 4를 기반으로 정식화한 비용 최적화 함수를 나타낸 것으로 크게 기본요금(Pb*Eb)과 시간대별 전력량요금(Lt–PVt+ESSt), 신재생에너지 요금할인(PVs), 그리고 ESS운영을 통한 경부하 /최대부하 구간에서의 전력량요금할인(ESSoff/ESSon)으로 구성되어 있다. 이외 제약조건은 동일하게 설정하였으며, 해당 수식을 바탕으로 1개월 간 전력운영비용을 산출하였다.
| $$f(P_\min)=P_{b\ast}E_b+(L_t-PV_t+ESS_t)-PV_s-ESS_{off}-ESS_{on}$$ | (7) |
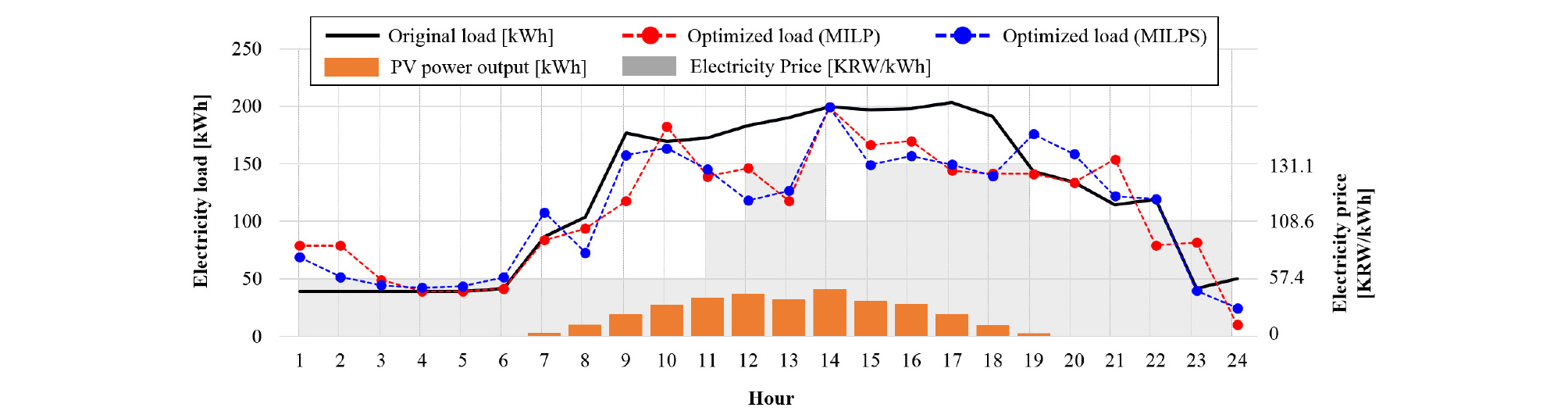
Figure 4는 선정된 MILP 기법을 기반으로 분산자원의 할인요금제도 적용 시 최대부하일의 시간별 전력소비량을 나타낸 것이다. MILP기법과 분산자원 할인요금 적용안(MILPS, Mixed-integer Linear Programming with subsidy)은 공통적으로 분산자원을 연계하지 않은 전력소비량(Original) 대비 최대부하 구간에서의 부하 감소특성이 뚜렷하며 중간부하 구간 내 부하특성은 각기 달랐다. MILPS 기법은 MILP 기법에 비해 중간부하 구간에서의 부하를 높이고 최대부하 구간에서의 부하를 감소시켜 비용을 최소화하는 특성을 나타냈다. 이후 MILPS 기법을 활용하여 장기간 그리드 운영 시 경제성을 평가하기 위해 1개월 간 전력요금을 산출하였다. Table 8은 1개월 간 전력소비량 및 운영비용을 나타낸 것이다. MILPS기법은 MILP 기법 대비 최대부하일과 동일하게 경부하 구간의 부하 특성은 유사하나 중간부하 구간의 전력소비량이 높고 최대부하 구간의 부하가 더 낮은 특성을 나타냈다. 이는 분산자원의 요금할인제도를 통해 최대부하 구간 내 전력운영비용 절감에 기여한 것으로 판단된다. 이를 통해 MILPS 기법의 1개월 간 전력요금(5,072천원)은 기존 전력소비량(Original)의 전력요금(8,108천원) 대비 37.45%의 비용 절감효율이 도출되었으며, MILP기법의 전력비용(7,278천원)에 비해 30.31%의 비용절감이 가능하였다.
Table 8. Optimization performance for electricity consumption and price with MILP method for 23 days in August based on discounted price system of DERs
결 론
본 연구에서는 초소형 마이크로그리드를 대상으로 세 가지 메타 휴리스틱 기법(MILP, GA, PS)의 성능비교를 통해 수요-분산자원 연계형 최적전력운영 전략을 수립하고 선정된 최적화 기법을 기반으로 국내 분산자원의 요금할인제도를 고려한 전력소비량 및 비용 절감 개선안을 제시하였다. 먼저, 세 가지 최적화 기법의 성능비교 결과, MILP 기법은 다른 최적화 기법에 비해 최적해 탐색 시간이 짧고 최적의 성능을 나타냈으며, 장기간(1개월 간)에서의 경제성 측면에서도 다른 기법 대비 최대 90천원의 전력운영비용 절감효과를 나타냈다. 이후 MILP 기법을 기반으로 분산자원의 요금할인을 고려한 1개월 간 전력운영비용 절감안을 수립하였다. 분산자원의 요금할인을 고려한 절감안 (MILPS)의 전력운영비용은 기존 MILP 기법 대비 30.31%의 절감효율이 도출되었고 분산자원을 연계하지 않은 기존안(Original) 전력운영비용에 비해 37.45%의 절감성능이 나타났다. MILPS 기법은 경부하/중간부하 구간의 ESS 충전을 통해 전력소비량을 높이고 최대부하 구간에서는 ESS의 최대방전을 통해 전력소비량을 감소시키는 특성으로 전략을 수립하였다.
상기 결과를 통해 그리드 설계단계에서 효율적인 전력 및 운영비용을 위해 최적화 기법의 선정의 기초자료로 활용이 가능하며 현재 시행되는 분산자원의 요금할인제도에 따른 효과적인 최적 전력운영기법을 제시할 수 있었다. 향후, 메타 휴리스틱 기법 이외 다양한 최적화 기법을 적용하여 그리드 간 특성에 적합한 기법을 탐색하고 분산-수요자원의 예측을 고려한 단기/중기 마이크로그리드 전력운영기법을 모색하고자 한다.