Global Sensitivity Analysis for ASHRAE Borehole Heat Exchanger Sizing Method

Euntak Shin; Yoonseong Kim; Wonjun Choi

doi:10.22696/jkiaebs.20230029

Preview

Research Article

Journal of Korean Institute of Architectural Sustainable Environment and Building Systems. 30 December 2023. 343-353
https://doi.org/10.22696/jkiaebs.20230029

Global Sensitivity Analysis for ASHRAE Borehole Heat Exchanger Sizing Method

ASHRAE 지열교환기 설계법에 대한 전역 민감도 분석

Euntak Shin¹

Yoonseong Kim²

Wonjun Choi³^*

신 은탁¹

김 윤성²

최 원준³^*

¹Undergraduate Student, School of Architecture, Chonnam National University, Gwangju, Korea

²Master’s Course Student, Department of Architecture and Civil Engineering, Chonnam National University, Gwangju, Korea

³Associate Professor, School of Architecture, Chonnam National University, Gwangju, Korea

¹전남대학교 건축학부 학부과정

²전남대학교 대학원 건축토목공학과 석사과정

³전남대학교 건축학부 부교수

^{*Corresponding Author}

ABSTRACT

Ground heat exchanger (GHE) is a critical component of ground-source heat pump systems. One of the most common GHE types is borehole heat exchanger (BHE). The determination of the required BHE length is influenced by many uncertain parameters, including the ground thermal load, ground thermal properties, and BHE geometry. The ground thermal load is influenced by the building loads and heat pump efficiency, which can vary widely. Spatially averaged ground thermal properties inherently involve uncertainty. Furthermore, the construction process for BHEs cannot be entirely controlled. The propagation of parameter uncertainties throughout the sizing process results in a significant level of uncertainty in estimating BHE length. Therefore, this study aims to quantify the contribution of each input parameter to BHE sizing, elucidating their impacts on BHE sizing uncertainty. The results exhibited that the 1-hour peak ground load and 720-hour-long peak ground load are the most influential factors contributing to BHE sizing uncertainty. Consequently, the results suggest that prioritizing uncertainty management of parameters related to ground load is essential to enhance the reliability of BHE design.

Keywords

Ground source heat pump

Global sensitivity analysis

Uncertainty quantification

ASHRAE borehole heat exchanger sizing method

키워드

지열히트펌프

전역 민감도 분석

불확실성 산정

ASHRAE 지열교환기 설계법

MAIN

서 론
연구 방법
대상 건물
ASHRAE 지열교환기 설계법
전역 민감도 분석
유한 선형 열원 모델
전역 민감도 분석 개요
결과 및 토의
지열교환기 설계 길이 불확실성
전역 민감도 분석 결과
결 론

서 론

수직 밀폐형 지열교환기(borehole heat exchanger (BHE))의 길이를 산정하는 방법은 크게 g-function기반의 반복적 설계법(Eskilson, 1987)과 ASHRAE (American Society of Heating, Refrigerating and Air-Conditioning Engineers) 설계법(Kavanaugh and Rafferty, 2014)으로 나뉜다. 이 두 가지 설계법 모두 지중에 할당되는 부하, 토양 열물성과 유효 보어홀 열저항, BHE와 보어홀의 형상에 관한 정보가 필요하다. 그러나 이들은 내재적으로 큰 불확실성을 갖는다.

지중에 할당되는 부하의 불확실성은 건물의 부하와 히트펌프 효율이 복합적으로 관여한다. 토양은 본래 공간적으로 비균질한 다공성 복합물질이나 지열에너지시스템 분야에서 공학적 편의성을 위해 공간 평균 열물성을 사용하는 것이 일반적이다. 또한 토양 열물성은 위치에 따라 크게 변화하며 현장 열응답 시험을 통해 역추론하기 때문에 근본적으로 불확실성에서 자유롭지 못하다. BHE의 시공 과정 또한 완벽하게 제어하는 것은 불가능하므로 BHE의 형상은 설계에서 가정한 것과 달라지게 된다. 이는 필요 BHE 길이 산정에 큰 영향을 주는 유효 보어홀 열저항을 불확실하게 한다(Choi et al., 2022).

BHE 필요 길이 산정과 관련된 파라미터가 근본적으로 불확실한 특성을 고려하면 파라미터 불확실성을 고려하여 설계를 확률론적으로 접근하는 것이 합리적이다. 확률론적 설계의 맥락에서 전역 민감도 분석법을 통해 각 입력 파라미터의 중요성을 정량화하는 것은 신뢰성 향상의 목적에서 유용하다. Choi et al. (2021)의 연구는 유효 보어홀 열저항의 추정을 불확실하게 하는 다양한 입력 파라미터의 기여도를 정량화하는 것을 통해 BHE 설계에 큰 영향을 주는 유효 보어홀 열저항의 추정 불확실성을 줄일 수 있고 궁극적으로 설계 신뢰성 향상으로 이어질 수 있음을 보였다.

본 연구에서는 ASHRAE 설계법에 기반한 확률론적 BHE 설계 사례를 제시한다. BHE 설계 길이의 불확실성에 관한 전역 민감도 분석을 수행하여 입력 파라미터가 BHE 필요 길이의 불확실성에 미치는 상대적인 영향력을 정량화한다. 본 연구의 결과는 BHE 설계 길이 산정 시 불확실성을 줄이기 위해 우선적으로 고려해야 할 요소에 대한 통찰을 제공함으로써 지열에너지 시스템의 설계 신뢰도를 높이는데 기여한다.

연구 방법

대상 건물

건물 부하를 산출하기 위하여 미국 에너지성(U.S. Department of Energy (DOE))에서 제공하는 Commercial Reference Building (U.S. Department of Energy, 2012)의 EnergyPlus (EnergyPlus, 2021) 모델 중 Small Office를 사용했다. Chicago의 기상 조건은 사계절이 뚜렷하여 균형 잡힌 냉난방 부하의 산출이 가능하기에 Chicago 지역의 Small Office를 사용했다. Small Office는 EnergyPlus의 입력 파일인 IDF (Input data file) 확장자 형태로 제공된다. DOE에서 제공하는 파일은 EnergyPlus 7.2 버전용으로 만들어졌으나 본 연구에서는 EnergyPlus 9.6 버전으로 변환하여 사용했다.

대상 건물의 공조 존은 동, 서, 남, 북 방위 별로 각 1개의 존과 코어 존으로 구성되어 있다. 그리고 비 공조 존인 Attic이 1층과 지붕 사이에 위치한다. 건물의 바닥면적은 511 m²이며 1층과 Attic의 층고는 각각 3.1 m, 3.23 m이다. Chicago O’Hare International Airport TMY3 (EnergyPlus, 2022) 기상 데이터를 시뮬레이션에 사용했다.

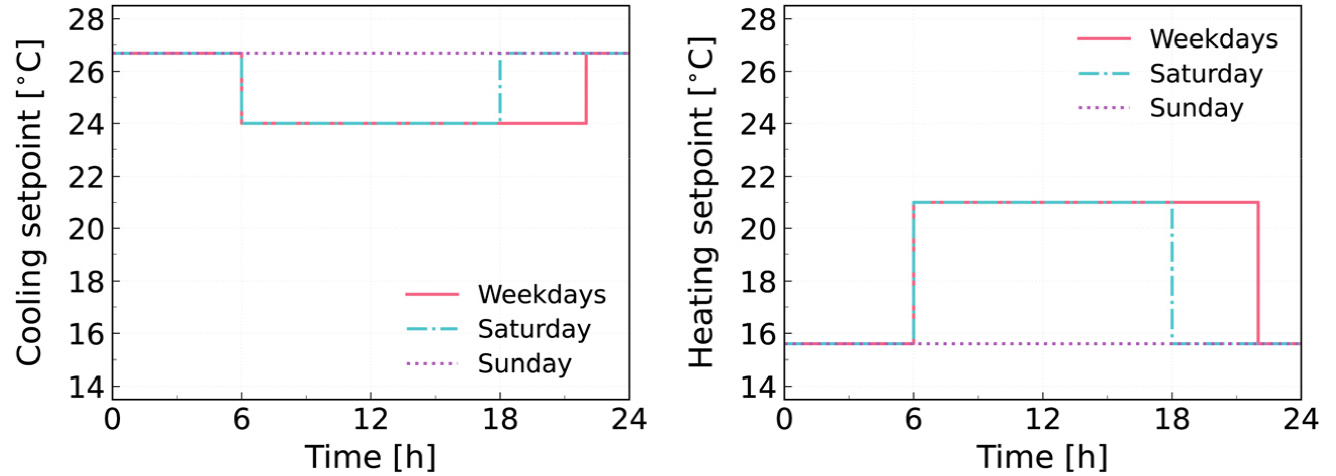
원본 IDF 파일에는 공기 열원 히트펌프와 가스 보일러가 공조설비로 입력되어 있다. 그러나 본 연구는 ASHRAE 설계식에서 요구하는 지중 부하를 산출하기 위한 건물 냉난방 부하를 얻는 것이 목적이다. 따라서 기존 입력된 공조 시스템 객체를 삭제하고, 100% 효율의 에너지 시스템을 모사하는 EnergyPlus 객체인 Ideal Air Load System으로 대체했다. 셋포인트 스케쥴은 평일, 토요일, 일요일이 서로 다르며 Figure 1과 같다.

https://cdn.apub.kr/journalsite/sites/kiaebs/2023-017-06/N0280170603/images/Figure_KIAEBS_17_6_03_F1.jpg

Figure 1.

Heating and cooling setpoint schedule of Small Office model

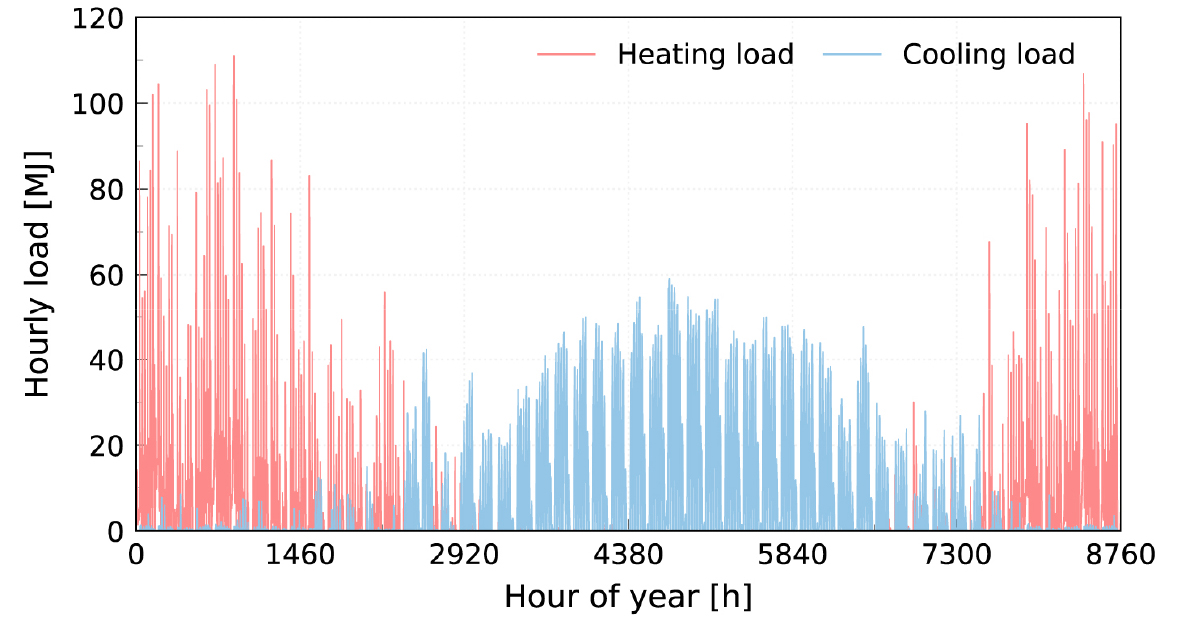
1년 시뮬레이션 결과에 대한 시간 단위 냉난방 부하는 Figure 2에 표시했다. 건물의 연간 냉방부하의 적분 값은 54.2 GJ로 연간 난방부하 26.6 GJ 보다 높지만 시간 단위 최대 부하는 난방부하가 111 MJ, 냉방부하가 59 MJ로 난방부하가 두 배 정도 크다. 필요 BHE 길이는 최대 부하에 지배적인 영향을 받기에(Rees, 2016) 본 연구는 난방을 위한 BHE 설계 길이 산정에 한정한다.

https://cdn.apub.kr/journalsite/sites/kiaebs/2023-017-06/N0280170603/images/Figure_KIAEBS_17_6_03_F2.jpg

Figure 2.

Heating and cooling load profile of Small Office model

ASHRAE 지열교환기 설계법

난방 운전에 대한 ASHRAE의 BHE 설계식은 다음과 같다(Kavanaugh and Rafferty, 2014).

(1)

L_{h} = \frac{q_{g, y} R_{g, 10 y} + q_{g, m} R_{g, m} + q_{g, 4 h} R_{g, 4 h} + q_{g, p e a k} R_{b}^{*}}{T_{g} - T_{f} - T_{p}}

(2)

q_{g} = q_{b} - \frac{q_{b}}{C O P}

식 (1)의 파라미터에 대한 설명은 Table 1에 기술했다. 본 연구에서는 분석의 복잡성을 줄이기 위해 복수의 BHE 사이의 열적 간섭이 없는 상황을 가정했다. 따라서 식 (1)의 파라미터 중 열적 간섭의 영향을 고려하기 위한 파라미터인 $T_{p}$ 는 0이 된다. 식 (1)의 $q_{g}$ 는 지중에 할당되는 부하를 의미하고 이는 식 (2)와 같이 건물에서 발생하는 부하인 $q_{b}$ 와 히트펌프의 $C O P$ (Coefficient of performance)에 의해 결정된다. 이는 서로 다른 네 가지 시간 길이의 지중 부하( $q_{g, p e a k}, q_{g, 4 h}, q_{g, m}, q_{g, y}$ )에 모두 적용된다.

Table 1.

Input parameters of ASHRAE sizing method

Symbol	Meaning	Unit
$L_{h}$	Required BHE length in heating operation	m
$q_{g, p e a k}$	Hourly peak ground load in heating	kW
$q_{g, 4 h}$	4-hour-long peak ground load in heating	kW
$q_{g, m}$	720-hour-long peak ground load in heating	kW
$q_{g, y}$	Annual average ground load in heating	kW
$R_{g, 4 h}$	Effective ground thermal resistance for a 4-hour-long heat pulse	(m·K)/W
$R_{g, m}$	Effective ground thermal resistance for a 720-hour-long heat pulse	(m·K)/W
$R_{g, 10 y}$	Effective ground thermal resistance for a 10-year-long heat pulse	(m·K)/W
$R_{b}^{*}$	Effective borehole thermal resistance	(m·K)/W
$T_{g}$	Initial ground temperature	°C
$T_{f}$	Mean BHE circulating fluid temperature	°C
$T_{p}$	Penalty temperature	°C
$C O P$	COP of heat pump	-

전역 민감도 분석

민감도 분석은 모델 출력의 불확실성에 대한 입력 파라미터들의 상대적인 영향력을 정량화하는 방법이다. 민감도 분석은 크게 전역 민감도 분석(Global sensitivity analysis)과 국소 민감도 분석(Local sensitivity analysis) 두 가지로 나눌 수 있다. 국소 민감도 분석은 특정 입력 파라미터가 가지는 임의의 값에 대한 편미분 결과에 기반하기 때문에 빠르게 결과를 얻을 수 있다. 그러나 파라미터 공간상의 임의 지점에서 편미분한 결과로 감도를 측정하기 때문에 모델이 비선형적인 경우 입력 파라미터 공간에서 선택한 값에 따라 결과가 크게 달라질 수 있다. 또한 이는 한 번에 하나의 파라미터만을 변화시키기 때문에 복수의 입력 파라미터가 동시에 변화하는 경우에 발생하는 파라미터 간의 상호작용을 고려할 수 없다. 이와 반대로 전역 민감도 분석은 입력 파라미터 공간 전체를 탐색할 수 있고 복수의 파라미터가 동시에 변화하는 경우의 영향을 고려할 수 있다. 따라서 입력 파라미터의 동시 변화와 파라미터 간 상호작용이 출력 변화에 미치는 영향을 산출할 수 있다.

본 연구에서는 전역 민감도 분석을 사용하여 BHE 설계 길이 불확실성에 대한 입력 파라미터의 영향력을 정량화한다. 전역 민감도 분석을 수행하는 방법은 크게 3가지로 나뉜다. 1) 회귀 분석 방법, 2) 변수 선별 방법, 3) 분산 분해 방법. 본 연구에서는 이 중에서 가장 계산 부하가 크지만 결과에 대한 신뢰성이 높은 분산 분해 방법 기반의 Sobol’s method (Sobol, 1993)를 사용했다.

Sobol’s method에서 제시하는 각 파라미터의 단일 효과 그리고 상호작용에 의한 영향은 Sobol 민감도 지수(Sensitivity index)로 나타낼 수 있다. Sobol 민감도 지수는 출력에 대한 특정 입력 파라미터의 단일 효과만을 고려한 1차 민감도 지수, 두 입력 파라미터 이상의 상호작용을 고려한 고차 민감도 지수로 나눌 수 있다. 1차 민감도 지수와 고차 민감도 지수를 모두 더한 것이 토탈 민감도 지수이다.

1차 민감도 지수는 $S_{i}$ 로 나타내며 이를 산정하는 식은 식 (3)과 같다.

(3)

S_{i} = \frac{V_{X_{i}} [{E_{X}}_{~ i} (Y | X_{i})]}{V (Y)}

식 (3) 우변 분자의 분산 연산자 ${V_{X}}_{i}$ 내부의 조건부 기댓값 ${E_{X}}_{~ i} (Y | X_{i})$ 의 하첨자 $X_{~ i}$ 는 $X_{i}$ 를 제외한 모든 입력 파라미터를 의미한다. 따라서 조건부 기댓값 ${E_{X}}_{~ i} (Y | X_{i})$ 는 $X_{i}$ 가 임의의 값을 가질 때 $N_{i}$ 이외 파라미터인 $X_{~ i}$ 의 변동에 의해 얻어지는 출력 $Y$ 의 평균값을 뜻한다. 조건부 기댓값에 취해지는 분산 연산자 ${V_{X}}_{i}$ 는 $X_{i}$ 가 가질 수 있는 모든 값에 대해 취해진다. 따라서 출력 $Y$ 의 분산 $V (Y)$ 에 대한 조건부 분산 ${V_{X}}_{i} [{E_{X}}_{~ i} (Y | X_{i})]$ 의 값이 클수록 $X_{i}$ 가 모델 출력의 불확실성에 미치는 영향이 크다는 것을 의미한다.

또한 Sobol’s method는 복수 파라미터 간의 상호작용 크기를 나타내는 고차 민감도 지수를 계산할 수 있으나, ASHRAE 설계식의 구조 상 2차 이상 민감도 지수의 크기는 무시할 수 있을 만큼 작을 것으로 예상했다. 따라서 계산 효율성을 높이고 분석을 간소화하기 위해 2차 이상의 민감도 지수를 별도로 산출하지 않고 1차와 토탈 민감도 지수만을 산출했다. 토탈 민감도 지수는 $S_{T_{i}}$ 로 나타내며 이는 식 (4)로 정의된다.

(4)

S_{T_{i}} = \frac{{E_{X}}_{~ i} [V_{X_{i}} (Y | X_{~ i})]}{V (Y)}

식 우변의 분자인 ${E_{X}}_{~ i} [V_{X_{i}} (Y | X_{~ i})]$ 는 $X_{~ i}$ 가 임의의 값을 가질 때 $X_{i}$ 만이 변화하여 얻어지는 출력 $Y$ 가 갖는 분산의 평균을 의미한다. 즉 $X_{i}$ 가 갖는 단일 효과와 다른 파라미터와의 상호작용에 의한 모든 효과를 합한 결과를 의미한다. 예를 들어 모델의 입력 파라미터를 $X = X_{1}, X_{2}, X_{3}$ 로 설정하면 파라미터 $X_{i}$ 에 대한 토탈 민감도 지수 $S_{T_{1}}$ 는 $S_{T_{1}} = S_{1} + S_{12} + S_{13} + S_{123}$ 이다.

본 연구에서는 1차 민감도 지수 $S_{i}$ 를 추정하기 위해 Saltelli et al. (2010)가 제안한 연산자를, 토탈 민감도 지수 $S_{T_{i}}$ 를 추정하기 위해 Jansen (1999)이 개발한 연산자를 사용했다.

유한 선형 열원 모델

ASHRAE 설계법(식 (1))의 입력 파라미터인 세 가지 유효 토양 열저항( $R_{g, 4 h}, R_{g, m}, R_{g, 10 y}$ )은 BHE에 열류가 할당되었을 때 시간이 지남에 따라 달라지는 토양의 저항으로 정의된다. 유효 토양 열저항을 산정하기 위해 수치적, 해석적 방법론을 사용할 수 있다. 전역 민감도 분석은 수천에서 수만 번의 모델 실행이 수반되기 때문에 수치적 모델 보다 계산 부하가 적은 해석적 모델을 사용했다. 해석적 모델 중 유한 선형 열원 모델(Claesson and Javed, 2011)을 사용했고 이는 식 (5)와 같다.

(5)

R_{g} (t) = \frac{1}{4 π k_{s}} \int_{1 / \sqrt{4 t k_{s} / C_{s}}}^{\infty} \exp (- r_{b}^{2} s^{2}) \frac{Y (H s, D s)}{H s^{2}} d s

여기서, $k_{s}$ : 유효 토양 열전도율, $C_{s}$ : 토양의 체적 열용량, : $1 / \sqrt{4 (t - t') k_{s} / C_{s}}$ , $H$ : BHE 활성 길이, $D$ : 지면으로부터 BHE의 유효 길이가 시작하는 매설 깊이, $r_{b}$ : 보어홀 반경, $t$ : 열 주입 이후 경과 시간을 의미한다. 식 (5)의 $Y$ 는 식 (6)와 같다.

(6)

Y (H s, D s) = 2 ierf (H s) + 2 ierf (H s + 2 D s) - ierf (2 H s + 2 D s) - ierf (2 D s)

식 (6) 우변의 ierf는 integral error function으로 식 (7)과 같이 정의된다.

(7)

ierf (x) = x e r f (x) - \frac{1}{\sqrt{π}} (1 - \exp (- x^{2}))

유한 선형 열원 모델을 이용해 세 가지 서로 다른 시간 스케일의 유효 토양 열저항( $R_{g, 4 h}, R_{g, m}, R_{g, 10 y}$ )을 산출할 때 시간 중첩 원리를 사용했다(Choi et al., 2019).

전역 민감도 분석 개요

ASHRAE 설계법에 대한 전역 민감도 분석을 위해 입력 파라미터들에 대한 불확실성을 확률 밀도 함수로 정의했다. 지중 부하의 불확실성을 산출하기 위해 확률 밀도 함수를 정의한 파라미터는 건물 부하 관련 파라미터와 히트펌프의 COP이다. 건물 부하 관련 파라미터는 단열재가 관입한 부위의 열관류율, 내부발열, 침기량, 창문의 일사획득계수(Solar heat gain coefficient (SHGC)), 창문의 열관류율이다. 할당한 불확실성 범위는 Table 2에 정리한 선행연구를 참고했으며 이들은 실험을 통한 추정 혹은 여러 문헌을 통해 조사한 값을 수록하고 있다. 다만 내부발열 요소 중 기기와 조명에 대한 불확실성 정의는 저자의 주관적 가정에 기반한다. 점유 공간의 조명과 기기 발열은 재실자 불확실성에 연동되어 각각 기준값에서 ±25%, ±30% 변동한다고 가정하고 이를 균등분포로 할당했다.

유효 토양 열저항의 불확실성을 산출하기 위해 식 (5)의 파라미터인 BHE 활성 길이( $H$ ), 보어홀 반경( $r_{b}$ ), 유효 토양 열전도율( $k_{s}$ )과 체적 열용량( $C_{s}$ )에 불확실성을 할당했다. 유효 토양 열저항에 영향을 미치는 파라미터의 확률 밀도 함수와 불확실성 범위 또한 선행연구를 참고하여 결정한 것으로 대부분 현장 열응답 시험 과정에서 발생할 수 있는 여러 불확실한 요인과 시공 오차에 근거한다. 상세는 Table 3에 요약했다.

Table 2.

Probability density functions for ground thermal load related parameters

Parameter [Unit]		Uncertainty range	Reference
Envelope U-value [W/(m²·K)]	Exterior wall	Uniform (0.78, 0.94)	ISO 9869-2 (2018)
Envelope U-value [W/(m²·K)]	Attic floor	Uniform (0.20, 0.24)	ISO 9869-2 (2018)
Internal heat gain [W/m²]	Occupancy	Uniform (4.3, 12.9)	Macdonald and Strachan (2001)
	Equipment	Uniform (7.5, 14.0)	-
	Lighting	Uniform (8.07, 13.45)	-
Zone infiltration [1/h]		Uniform (0.02, 0.32)	Pettersen (1997)
Window U-value [W/(m²·K)]		Normal (3.24, 0.20)	Hopfe (2009)
Window SHGC		Uniform (0.39, 0.45)	Wright (1995)
COP of heat pump		Uniform (3.0, 4.3)	Spitler et al. (2017)

Table 3.

Probability density functions for effective ground thermal resistance related parameters

Parameter [Unit]	Uncertainty range	Reference
BHE active length [m]	Uniform (99.9, 100.1)	Choi et al. (2021)
Borehole radius [m]	Uniform (0.070, 0.085)	Choi et al. (2021)
Ground thermal conductivity [W/(m·K)]	Uniform (1.8, 2.2)	Choi et al. (2021)
Ground volumetric heat capacity [kJ/(m³·K)]	Uniform (1875, 3125)	Choi et al. (2021)

유효 토양 열저항에 영향을 미치는 파라미터에 대한 불확실성을 할당하고 식 (4)에 대한 몬테카를로 시뮬레이션을 통해 세 가지 서로 다른 시간 스케일의 토양 열저항( $R_{g, 4 h}, R_{g, m}, R_{g, 10 y}$ )의 확률 밀도 함수를 얻었다.

Table 2의 파라미터 셋을 이용해 산정한 네 가지 시간 길이의 지중 부하( $q_{g, p e a k}, q_{g, 4 h}, q_{g, m}, q_{g, y}$ ) 와 Table 3의 파라미터 셋을 이용해 산정한 세 가지 시간 스케일의 유효 토양 열저항( $R_{g, 4 h}, R_{g, m}, R_{g, 10 y}$ )을 포함하여 ASHRAE 설계법에 사용된 모든 파라미터에 대한 확률 밀도 함수와 범위를 Table 4에 기술했다.

Table 4.

Parameters for the global sensitivity analysis using the ASHRAE sizing method and their uncertainty ranges

Parameter [Unit]	Uncertainty range
$q_{g, p e a k}$ [kW]	Uniform (21.6, 29.0)
$q_{g, 4 h}$ [kW]	Uniform (13.1, 19.8)
$q_{g, m}$ [kW]	Uniform (1.9, 5.4)
$q_{g, y}$ [kW]	Uniform (0.7, 2.3)
$R_{b}^{*}$ [(m·K)/W]	Uniform (0.108, 0.132)
$R_{g, 4 h}$ [(m·K)/W]	Uniform (0.7, 2.3)
$R_{g, m}$ [(m·K)/W]	Uniform (0.18, 0.22)
$R_{g, 10 y}$ [(m·K)/W]	Uniform (0.15, 0.19)
$T_{f}$ [°C]	Uniform (3.8, 4.2)
$T_{g}$ [°C]	Uniform (14.3, 15.7)

https://cdn.apub.kr/journalsite/sites/kiaebs/2023-017-06/N0280170603/images/Figure_KIAEBS_17_6_03_F3.jpg

Figure 3.

Probability density function of borehole heat exchanger design length

결과 및 토의

지열교환기 설계 길이 불확실성

Table 4에서 제시한 파라미터의 불확실성 범위로부터 샘플링한 입력 파라미터 셋을 이용해 몬테카를로 시뮬레이션을 실시했고 산출한 BHE 설계 길이의 확률 밀도 함수는 Figure 3과 같다. 난방 운전 시 필요 BHE 길이의 95% 신뢰 구간은 382.3 ~ 549.4 m이다. 95% 신뢰 구간이 382.3 ~ 549.4 m이라는 것은 한 공의 BHE가 150 m의 길이로 시공된다고 가정했을 때 BHE를 세 공을 설치할지, 아니면 네 공을 설치할지에 대한 의사결정이 필요함을 의미한다. 건축주가 BHE 세 공을 선택하는 경우 설치 초기 비용을 절약할 수 있으나 히트펌프의 출력이 불충분할 수 있다. 이와 반대로 BHE 네 공을 설치하는 경우 초기비용은 상승하나 히트펌프 출력 부족의 가능성은 현저하게 낮아진다. 따라서 입력 파라미터를 확률변수로 다뤄 확률론적 설계를 수행하는 것은 엔지니어 혹은 건축주가 명확한 근거자료에 기반하여 의사결정을 할 수 있도록 돕는다.

전역 민감도 분석 결과

BHE 설계 길이 불확실성에 대한 전역 민감도 분석을 수행한 결과 1차와 토탈 민감도 지수 사이에 유의미한 차이가 없음을 확인했다. 따라서 민감도 분석의 결과로써 1차 민감도 지수만을 제시하였고 백분율로 변환하여 Figure 4에 나타냈다.

1차 민감도 지수가 높은 순으로 나열하면 연중 1시간 최대 지중 부하( $q_{g, p e a k}$ ), 720시간 평균 최대 지중 부하( $q_{g, m}$ ), 토양의 초기 온도( $T_{g}$ ), 유효 보어홀 열저항( $R_{b}^{*}$ ), 4시간 지중 히트 펄스에 대한 유효 토양 열저항( $R_{g, 4 h}$ ), 4시간 평균 연간 최대 지중 부하( $q_{g, 4 h}$ ), 1년 평균 지중 부하( $q_{g, y}$ ), BHE 순환 유체의 히트펌프 평균 입출구 온도( $T_{f}$ ), 720시간 지중 히트 펄스에 대한 유효 토양 열저항( $R_{g, m}$ ), 10년 지중 히트 펄스에 대한 유효 토양 열저항( $R_{g, 10 y}$ ) 순이다.

https://cdn.apub.kr/journalsite/sites/kiaebs/2023-017-06/N0280170603/images/Figure_KIAEBS_17_6_03_F4.jpg

Figure 4.

First-order sensitivity index for ASHRAE method parameters

일반적으로 BHE 설계에서 지중 부하는 고정된 값으로 간주되고 불확실성 분석의 초점은 대부분 토양의 열물성과 같은 지중 파라미터에 맞춰져 있다. 그러나 전역 민감도 분석 결과 연중 1시간 최대 지중 부하의 영향력이 가장 크다는 것을 확인했다. 이는 부하의 불확실성을 줄이는 것이 토양 열물성 파라미터의 불확실성을 줄이는 것보다 BHE 설계 길이의 신뢰성 향상에 더 큰 영향력을 가질 수 있음을 시사한다. 따라서 BHE 설계의 신뢰성을 높이기 위해서는 지중 할당 부하 산정의 정확성 향상에 대한 고민이 우선되어야 한다. 또한 지중 할당 부하는 건물에서 발생하는 부하에 기반하기에 향후 건물 부하 관련 파라미터에 대한 불확실성 분석이 추가로 수행되어 ASHRAE 설계법과 통합되어야 할 것이다.

결 론

본 연구에서는 ASHRAE 설계법을 이용한 확률론적 설계와 입력 파라미터에 대한 전역 민감도 분석을 수행했다. 난방 운전 시 필요 지열교환기 길이를 확률론적으로 산정하면 추정된 필요 길이에 대한 확률 밀도 함수를 얻을 수 있다. 이를 통해 지열교환기를 몇 공 설치할 것인지에 대한 판단 근거로 활용할 수 있음을 보였다.

지열교환기 설계 길이 추정 불확실성에 대한 전역 민감도 분석을 수행한 결과 연중 1시간 최대 지중 부하의 영향력이 약 29.6%로 가장 높게 나타났다. 그 뒤로 영향력이 큰 순으로 나열하면 720시간 평균 연간 최대 지중 부하, 토양의 초기 온도, 유효 보어홀 열저항, 4시간 히트 펄스에 대한 유효 토양 열저항, 4시간 평균 연간 최대 지중 부하, 지열교환기 순환 유체의 히트펌프 평균 입출구 온도 , 720시간 지중 히트 펄스에 대한 유효 토양 열저항, 10년 지중 히트 펄스에 대한 유효 토양 열저항의 순이다.

본 연구의 결과는 지열교환기 설계 신뢰도를 높이는 목적에서 지중 피크 부하의 불확실성을 관리하는 것이 가장 효과적임을 시사한다. 지중 부하는 건물 부하에 직접적인 영향을 받기에 건물 부하와 관련된 파라미터를 ASHRAE 설계식의 하위 파라미터로 포함하는 확장된 연구가 향후 수행되어야 할 것이다. 또한 건물의 규모, 기후 조건을 달리하면 네 가지 시간 길이의 부하 크기와 상대적인 비율이 달라질 것이고 이는 전역 민감도 분석 결과의 변화로 이어질 것이다. 체계적인 조건 설정과 분석을 통해 부하 특성에 따른 지열교환기 설계 관련 파라미터의 기여도 변화를 정량화하는 연구가 향후 수행되어야 한다.

Acknowledgements

이 논문은 정부(과학기술정보통신부)의 재원으로 한국연구재단(No. RS-2023-00277318)의 지원과 전남대학교 학술연구비(No. 2022-2664)의 지원으로 수행한 연구임.

References

Choi, W., Choudhary, R., Ooka, R. (2021). Development of chiller-attached apparatus for accurate initial ground temperature measurement: Insights from global sensitivity analysis of thermal response tests. Energy and Buildings, 238, 110841. 10.1016/j.enbuild.2021.110841

Choi, W., Kikumoto, H., Ooka, R. (2019). Critical comparison between thermal performance test (TPT) and thermal response test (TRT): Differences in heat transfer process and extractable information. Energy Conversion and Management, 199, 111967. 10.1016/j.enconman.2019.111967

Choi, W., Kikumoto, H., Ooka, R. (2022). Probabilistic uncertainty quantification of borehole thermal resistance in real-world scenarios. Energy, 254, 124400. 10.1016/j.energy.2022.124400

Claesson, J., Javed, S. (2011). An Analytical Method to Calculate Borehole Fluid Temperatures for Time-scales from Minutes to Decades. ASHRAE Transactions, 117(2), 279-288.

Jansen, M.J. (1999). Analysis of variance designs for model output. Computer Physics Communications, 117(1-2), 35-43. 10.1016/S0010-4655(98)00154-4

MacDonald, I., Strachan, P. (2001). Practical application of uncertainty analysis. Energy and Buildings, 33(3), 219-227. 10.1016/S0378-7788(00)00085-2

Saltelli, A., Annoni, P., Azzini, I., Campolongo, F., Ratto, M., Tarantola, S. (2010). Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Computer Physics Communications, 181(2), 259-270. 10.1016/j.cpc.2009.09.018

Sobol, I.M. (1993). Sensitivity estimates for nonlinear mathematical models. Mathematical Modelling and Computational Experiments, 1(4), 407-414.

Wright, J.L. (1995). Summary and comparison of methods to calculate solar heat gain. ASHRAE Transactions, 1, 802-818.

Spitler, J.D., Southard, L.E., Liu, X. (2017, May). Ground-source and air-source heat pump system performance at the ASHRAE headquarters building. Paper presented at the 12th IEA Heat Pump Conference: International Energy Agency. Rotterdam, Netherlands.

Kavanaugh, S.P., Rafferty, K.D. (2014). Geothermal heating and cooling: design of ground-source heat pump systems. Atlanta: ASHRAE, 51-89.

Rees, S. (2016). Advances in ground-source heat pump systems. Amsterdam: Woodhead Publishing.

Eskilson, P. (1987). Thermal analysis of heat extraction boreholes. PhD Thesis. University of Lund, Sweden.

Hopfe, C.J. (2009). Uncertainty and sensitivity analysis in building performance simulation for decision support and design optimization. PhD Thesis. Technische Universiteit Eindhoven, The Netherlands.

Pettersen, T.D. (1997). Uncertainty analysis of energy consumption in dwellings. PhD Thesis. Norwegian University of Science and Technology Trondheim, Norway.

ISO 9869-2. (2018). Building Elements - In-Situ Measurement of Thermal Resistance and Thermal Transmittance - Part 2: Infrared method for frame structure dwelling.

EnergyPlus. (2021). Version 9.6.0. Available at: https://energyplus.net/.

EnergyPlus. (2022). Weather Data by Location: Chicago-O'Hare International Airport 725300 (TMY3), Available at: https://energyplus.net/weather-location/north_and_central_america_wmo_region_4/USA/IL/USA_IL_Chicago-OHare.Intl.AP.725300_TMY3.

U.S. Department of Energy. (2012). New Construction-Commercial Reference Buildings. Available at: https://www.energy.gov/eere/buildings/new-construction-commercial-reference-buildings.

Journal of Korean Institute of Architectural Sustainable Environment and Building SystemsISSN:1976-6483(Print) 2586-0666(Online)한국건축친환경설비학회

Preview

Global Sensitivity Analysis for ASHRAE Borehole Heat Exchanger Sizing Method

ABSTRACT

MAIN

Figure 1.

Heating and cooling setpoint schedule of Small Office model

Figure 2.

Heating and cooling load profile of Small Office model

(1)

(2)

Table 1.

Input parameters of ASHRAE sizing method

(3)

(4)

(5)

(6)

(7)

Table 2.

Probability density functions for ground thermal load related parameters

Table 3.

Probability density functions for effective ground thermal resistance related parameters

Table 4.

Parameters for the global sensitivity analysis using the ASHRAE sizing method and their uncertainty ranges

Figure 3.

Probability density function of borehole heat exchanger design length

Figure 4.

First-order sensitivity index for ASHRAE method parameters

Acknowledgements

References