Result Comparison of Internal Condensation Evaluation method through EN 15026 Benchmark Test

Da-Hye Min; Young-Tag Kim; Young-Cheol Kwon; Dong-Chul Yoo; Hyang-In Jang

doi:10.22696/jkiaebs.20200013

Preview

Research Article

Journal of Korean Institute of Architectural Sustainable Environment and Building Systems. 28 February 2020. 136-146
https://doi.org/10.22696/jkiaebs.20200013

Result Comparison of Internal Condensation Evaluation method through EN 15026 Benchmark Test

EN 15026 Benchmark Test를 통한 내부결로 평가방법의 해석결과 비교

Da-Hye Min¹

Young-Tag Kim²

Young-Cheol Kwon³

Dong-Chul Yoo⁴

Hyang-In Jang⁵^*

민 다혜¹

김 영탁²

권 영철³

유 동철⁴

장 향인⁵^*

¹Researcher, Institute of Green Building and New Technology, Mirae Environment Plan

²Executive Director, Business Operation Group, AIMT co. Ltd.

³Professor, Department of Architecture, Halla University

⁴General Manager, Institute of Green Building and New Technology, Mirae Environment Plan

⁵Director, Institute of Green Building and New Technology, Mirae Environment Plan

¹(주)미래환경플랜건축사사무소 건축친환경기술연구소 연구원

²에임트 주식회사 사업운영그룹 이사

³한라대학교 건축학과 교수

⁴(주)미래환경플랜건축사사무소 건축친환경기술연구소 실장

⁵(주)미래환경플랜건축사사무소 건축친환경기술연구소 연구소장

^{* Corresponding Author}

License (open-access):

Ⓒ 2020 Korean Institute of Architectural Sustainable Environment and Building Systems. This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons. org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

As condensation is recognized as a major problem and defect in buildings, There is a need for an accurate evaluation method and criteria for determining condensation. However, in Korea, there is no evaluation criteria other than whether surface condensation using TDR occurs in a steady state. Therefore, The study considered methods for evaluating internal condensation in abnormal conditions and compared and analyzed the EN 15026 benchmark results. Comparing the evaluation index of EN 15026 and the calculated values of the researched evaluation method, the overall distribution of the temperature and the moisture content and the shape of the graph were calculated and analyzed very similarly. Later, the researched Matsumoto Mamoru algorithm is applied to reduce condensation in the initial design, and further research on the analysis of various structures will be performed.

Keywords

Internal Condensation

Evaluation method

EN15026

Benchmark Test

키워드

내부결로

평가방법

EN 15026

Benchmark Test

MAIN

서 론
연구배경 및 목적
연구방법 및 절차
이론적 고찰
ISO 13788
EN 15026
Matsumoto Mamoru의 기초방정식
ISO 13788, EN 15026, Matsumoto Mamoru의 기초방정식
EN 15026 (Annex : Benchmark Test)
개요
Benchmark Test 수행결과
결 론

서 론

연구배경 및 목적

결로는 건물에서 발생하는 주요 현상으로 표면결로와 내부결로로 구분된다. 표면결로는 외피 실내 측에서 주로 발생하는 현상으로 곰팡이와 같은 주요 하자 증상으로 연결된다. 내부결로는 건축물 외피 구조체의 함수율에 따라, 동결(응결) 및 팽창의 반복작용을 통하여 공극 또는 균열에 의해 구조의 안정성이 저하된다. 이와 같이 결로에 의한 피해를 해결하기 위하여 국외의 ISO 13788 (2007)과 EN15026 (2007)에서는 열· 습기 특성을 동시에 고려하여 표면결로와 내부결로를 평가할 수 있도록 규정하고 있다. ISO 13788은 건축물 부위별로 수증기압 차에 의해 발생하는 투습량을 산출하고, 이를 통해 월별 결로량을 계산할 수 있으나, 특정 시간의 결로량은 계산할 수 없다. 반면 EN 15026은 기후데이터를 활용하여 건축물 구조체의 수증기 확산과 액체 전달에 의한 수분이동을 예측할 수 있어 연간 시간별 결로량을 산출할 수 있는 평가방법을 제시하고 있다. 한편, 국내의 ‘공동주택 결로 방지를 위한 설계기준’은 연간 기후데이터가 아닌 정상상태로 평가(국토교통부, 2016)하며, 중부지역 기준으로 –15℃, 실내온도 25℃, 상대습도 50%를 가정하여 적용하고 있다. 각 부위별 결로 발생 여부는 TDR (Temperature Difference Ratio: 온도차이비율)이라는 지표를 사용하여 정상상태의 표면결로만을 판정하고 있다. 결로 평가 시 정상상태 해석은 온도분포와 각 온도의 포화수증기압만을 평가하기 때문에 시간에 따른 구조체 내부의 온습도 및 함수율 변화를 예측할 수 없으며, 이는 실제 발생하는 결로 현상보다 과도하게 결로가 발생하는 것으로 계산된다.

즉, 국내의 결로계산은 정상상태의 표면 결로만 해석되고 있고, 국외 기준과 같이 정상상태의 내부결로 및 기후데이터를 활용하는 비정상상태의 해석은 부재한 상황이다.

이에 본 연구는 국내 내부결로 판단 기준 및 방법론 개선에 기여하고자 국외의 정상 및 비정상상태의 내부결로 해석방법을 비교 조사하고, 국내에서 활용 가능한 계산 방법을 검증하고자 한다.

연구방법 및 절차

본 연구는 국내 내부결로 평가툴을 개발하기 위해, 국외의 정상 및 비정상상태의 평가방법을 조사하였다. 특히 비정상상태에 관한 내부결로 평가 방법은 EN 15026에서 제시하는 Benchmark Test에 근거하여 추후 활용하고자 하는 열 및 수분 동시이동방정식(일본의 Motsumoto Mamoru가 제안한 기초방정식)을 비교 분석하여 그 타당성을 검증하고자 하며, 본 연구의 구체적인 수행 절차는 다음과 같다.

(1) 이론적 고찰(내부결로 평가 방법 고찰 및 분석)

- ISO 13788(정상상태) 내부결로 평가 방법 고찰

- EN 15026(비정상상태) 내부결로 평가 방법 고찰

- Matsumoto Mamoru의 기초방정식(비정상상태) 내부결로 평가방법 고찰

(2) Benchmark Test 분석

- 기존 사용프로그램(WUFI) Benchmark Test Review

- Matsumoto Mamoru 기초방정식의 Benchmark Test 결과

(3) 오차율 분석

- EN 15026 Benchmark Test 지표와 Matsumoto Mamoru 기초 방정식

이론적 고찰

ISO 13788

ISO 13788은 표면결로와 내부결로를 판단하기 위해 수증기압 차이에 의한 결로 누적량 계산방법을 제시하고 있다. 정상상태의 내부결로 계산은 월평균 온습도 조건에 따라 구조체 내부의 온도 분포를 계산하고 각 경계층의 온도에 따른 포화수증기압을 식 (1), 식 (2)를 사용하여 산출한다.

$$p_{sat}=610.5e^\frac{17.269\theta}{237.3+\theta}\;\;\;\;\;\;\;\;\;\;(T\geq\;0^\circ\mathrm c)$$

(1)

$$p_{sat}=610.5e^\frac{21.875\theta}{265.5+\theta}\;\;\;\;\;\;\;\;\;\;(T<\;0^\circ\mathrm c)$$

(2)

구조체를 구성하는 재료 경계층에서의 수증기압( $P_{c}$ )은 정상상태의 실내외 수증기압차를 이용하여 산출하고, 수증기압( $P_{c}$ )이 해당 경계층의 포화수증기압( $P_{s a t}$ )을 초과하면 내부결로가 발생한 것으로 판단하며(Hong et al., 2017) 식(3)과 같이 산출한다.

g_{c} = g_{i, c} - g_{c, e} = δ_{0} (\frac{P_{i} - P_{c}}{{S^{'}}_{d, T} - {S^{'}}_{d, c}} - \frac{P_{c} - P_{c}}{{S^{'}}_{d, c}})

(3)

$θ$	: Temperature	[℃]
$p_{s a t}$	: Saturated water vapor pressure	[Pa]
$p_{c}$	: Surface water vapor pressure Exceeding $p_{s a t}$	[Pa]
$p_{i}$	: Internal water vapor pressure	[Pa]
$p_{e}$	: External water vapor pressure	[Pa]
${S^{'}}_{d, T}$	: Water vapour diffusion-Equivalent whole building Wall thickness	[m]
${S^{'}}_{d, c}$	: Water vapour diffusion-Equivalent $p_{c}$ thickness	[m]
$δ_{0}$	: Water vapour permeability of material with respect to partial vapour pressure	[kg/m‧s‧Pa]
$g_{c}$	: Density of water vapour flow rate in $p_{c}$	[kg/m²s]
$g_{i, c}$	: Density of water vapour flow rate from indoor $p_{i}$ to $p_{c}$	[kg/m²s]
$g_{c, e}$	: Density of water vapour flow rate from $p_{c}$ to outdoor $p_{e}$	[kg/m²s]

ISO 13788은 정상상태의 온습도 조건하에서 온도와 수증기압 분포를 별도 계산하여 연간 누적 결로량을 산출한다. 내부결로는 재료의 공극에 수증기가 포화상태에 도달하여 수분이 축적되는 현상이므로 공극의 용적 이상으로 결로가 발생하면 액체상태의 이동이 발생하는데, 정상상태에서는 이러한 현상을 설명할 수 없다.

EN 15026

EN 15026은 열과 습기의 이동을 고려한 결로를 판단하기 위해 수증기 확산과 액체 전달에 의한 결로 계산방법을 제시하고 있다. 시간에 따른 실내외 경계조건과 구조체의 재료의 물성값이 고려되며(Kim et al., 2017) 수분이동은 기체상태와 액체상태로 이동하며 구조체 내부의 함수율 상태를 판단할 수 있다.

EN 15026에서 제시하는 열 및 수분 이동에 관한 기초방정식은 다음과 같다. 열의 이동은 식 (4)와 같이 현열( $q_{s e n s}$ )과 잠열( $q_{l a t}$ )의 이동을 고려하였고, 재료 내부의 함수율 변화에 따른 수분의 이동은 식 (5)와 같이 기체 상태( $g_{v}$ )와 액체상태( $g_{l}$ )로 이동하는 것을 표현하고 있다. 또한, 실내 및 외기 공기와 재료 표면 사이의 열 및 수분 이동은 외부 기상 조건(일사량 및 장파복사량)을 반영한 등가 온도( $T_{e q}$ )와 재료 표면 온도 차이에 의해 식 (4)와 같이 열이 이동하고, 수분은 공기와 재료 표면의 수증기압 차이에 의해 식 (5)와 같이 이동하는 것으로 기초방정식이 구성되어있다.

$$\rho c\frac{\partial T}{\partial t}=-\frac\partial{\partial x}(q_{sens}+q_{lat})=\frac\partial{\partial x}(\lambda\frac{\partial T}{\partial x}+r\lambda'\frac{\partial p_v}{\partial x})$$

(4)

$$\rho_w\frac{\partial\phi}{\partial t}=-\frac\partial{\partial x}(g_v+g_l)=\frac\partial{\partial x}(\lambda'\frac{\partial p_v}{\partial x}+K(p_{suc})\frac{\partial p_{suc}}{\partial x})$$

(5)

$$q_{sens}=\alpha(T_{eq}-T_{surf})\;(\mathrm{Boundary}\;\mathrm{condition}\;\mathrm{of}\;\mathrm{heat}\;\mathrm{flux})$$

(6)

$$g_v=\frac{\delta_o}{s_{d,s}}(p_{v,a}-p_{v,s})\;(\mathrm{Boundary}\;\mathrm{condition}\;\mathrm{of}\;\mathrm{moisture}\;\mathrm{flux})$$

(7)

한편, 재료 내부의 수분 이동과 관련하여 기체상태의 수분 이동은 수증기압의 차이로 이동하고, 액체상태의 수분 이동은 재료 공극(pore)의 수증기압과 주변 공기의 압력 차이에 의해 발생하는 모세관현상(capillary forces)에 의해 이동하는데, 이는 온도와 상대습도에 의해 좌우되며 식 (8)을 참고할 수 있다.

$$P_{suc}=f(T,h)=-\rho_wR_vT\;ln(h)$$

(8)

$T$	: Temperature	[K]
t	: Time	[s]
$ρ$	: Density	[kg/㎥]
$c$	: Specific heat capacity	[J/kgK]
r	: Specific latent enthalpy of evaporation or condensation	[J/kg]
$q_{s e n s}$	: Density of sensible heat flow rate	[W/㎡]
$q_{l a t}$	: Density of latent heat f1ow rate	[W/㎡]
$λ$	: Thermal conductivity	[W/mK]
$p_{v}$	: Vapour pressure	[Pa]
$\emptyset$	: Water content of volume rate (= $(w - w_{0}) / ρ_{w} V$ )	[-]
$ρ_{w}$	: Density of water	[kg/㎥]
$g_{v}$	: Density of water vapor flow rate	[W/㎡s]
$g_{l}$	: Density of liquid water f1ow rate	[W/㎡s]
$λ'$	: Vapour permeability of material	[kg/msPa]
$h_{e}$	: Specific latent enthalpy of evaporation or condensation	[J/kg]
$K$	: Liquid conductivity = $- D_{w} (ρ_{w} \emptyset) \frac{\partial}{\partial p_{s u c}} (ρ_{w} \emptyset)$	[kg/msPa]
$P_{s u c}$	: Suction pressure	[Pa]
$T_{e q}$	: Equivalent temperature of the surrounding environment	[K]
$T_{s u r f}$	: Surface temperature	[K]
$δ_{0}$	: Vapour permeability of still air	[kg/msPa]
$s_{d, s}$	: Equivalent vapour diffusion thickness of a surface layer	[m]
$R_{v}$	: Gas constant for water vapour	[J/kgK]
$h$	: Relative humidity	[-]

EN 15026의 기초방정식의 확산계수 $λ$ , $λ'$ , $K$ 는 함수율에 의존한다. 함수율은 온도 및 습도에 관한 함수인데, 온도에 의한 영향은 미비하여 일반적으로 식 (9)와 같이 상대습도의 함수로 표현한다.

$$\phi=f(T,h)\simeq f(h)$$

(9)

Matsumoto Mamoru의 기초방정식

Matsumoto Mamoru (1984) 등에 의하여 제안된 열 및 수분 동시 이동방정식의 구성은 다음과 같다. 수분의 포텐셜이 기체상태와 액체상태에 항상 평형상태(국소 평형상태)를 유지할 경우, 열 및 수분 포텐셜 구배에 비례하는 유량과, 열과 수분의 상호 영향에 의해서 발생하는 유량과의 중첩 효과에 의해서 식 (10)과 같이 나타낼 수 있다.

$$\begin{bmatrix}q\\J\end{bmatrix}=-\begin{bmatrix}D_{\;TT}&D\;_{TX}\\D_{\;XT}&D_{\;XX}\end{bmatrix}\begin{bmatrix}\nabla T\\\nabla X\end{bmatrix}$$

(10)

$q$	: Heat Flow rate	[W/㎡]
$J$	: Water Flow rate	[㎏/㎡s]
$D$	: Diffusion Coefficient
$\nabla$	: Differential Operator
$T$	: Heat Potential Energy	[K]
$X$	: Water Potential Energy	[㎏]

수분 이동의 종류에는 기체상태의 이동과 액체상태의 이동이 있고, 수분의 포텐셜(구동력)에는 분자농도에 비례하는 수증기압, 수분의 화학포텐셜 또는 이와 비례하는 상대습도, 절대습도 등이 있다. 본 연구에서 이용하는 Matsumoto Mamoru의 열 및 수분 동시 이동방정식은 시간에 따른 수분의 화학포텐셜 $μ$ 을 사용하는 방정식으로, 외력이 존재하지 않은 1차원에서 열의 이동은 식 (11)로 재료 내부의 함수율 변화에 따른 수분의 이동은 식 (12)와 같이 표현된다.

ρ c \frac{\partial T}{\partial t} = \frac{\partial}{\partial x} \{(λ + r λ_{T g}^{'}) \frac{\partial T}{\partial x} + r λ_{μ g}^{'} \frac{\partial μ}{\partial x}\}

(11)

ρ_{w} \frac{\partial ϕ}{\partial μ} \frac{\partial μ}{\partial t} = \frac{\partial}{\partial x} (λ_{μ}^{'} \frac{\partial μ}{\partial x} + r λ_{T}^{'} \frac{\partial T}{\partial x})

(12)

$$\lambda'_\mu=\lambda'_{\mu g}+\lambda'_{\mu l}\;\;\;\;\;\lambda'_{\mu g}=\frac{p_{vs}h}{R_vT}\lambda'\;\;\;\;\;\lambda'_{\mu l}=D_{\phi l}\frac h{R_vT}\frac{\partial\phi}{\partial h}$$

(13)

$$\lambda'_T=\lambda'_{Tg}+\lambda'_{Tl}\;\;\;\;\;\lambda'_{Tg}=\frac{dp_{vs}}{dT}h\lambda'\;\;\;\;\;\lambda'_{Tl}=D_{Tl}$$

(14)

$$\alpha'_\mu=\frac{\alpha_c}{\rho cR_vT}\frac{\partial p_v}{\partial\mu}\;\;\;\;\;\alpha'_T=\frac{\alpha_c}{\rho cR_vT}\frac{\partial p_v}{\partial T}$$

(15)

$μ$	: Chemical Potential of Water	[J/kg]
$\emptyset$	: Volume Water Content	[Vol%]
$λ$	: Thermal Conductivity	[W/mK]
$λ'_{μ}$	: Vapor Conductivity	[kg/msPa]
$λ'$	: Vapor Conductivity by $μ$ gradient	[㎏/ms(J/kg)]
$λ'_{T}$	: Vapor Conductivity by $T$ gradient	[㎏/msK]
$D_{\emptyset l}$	: Water Conductivity by $\emptyset$ gradient	[㎏/ms-]
$D_{T l}$	: Water Conductivity by $T$ gradient	[㎏/msK]
$ρ$	: Density of material	[kg/㎥]
$c$	: Specific heat of material	[J/kgK]
$h$	: Relative Humidity	[%]
[Subscript]	$_{g}$ : gas phase, $_{l}$ : liquid phase, $_{w}$ : water, $_{o}$ : outdoor, $_{s o}$ : outside surface $_{c}$ : convective heat transfer, $_{r}$ : radiative heat transfer

ISO 13788, EN 15026, Matsumoto Mamoru의 기초방정식

본 장은 내부결로 평가 시 활용되는 인자를 ISO 13788, EN 15026, Matsumoto Mamoru에 기반을 둔 기초방정식에 따라 분류하였으며 해당 항목의 차이를 Table 1과 같이 정리하였다.

Table 1. Standard Compare table

Evaluation Standard			ISO 13788	EN 15026	Matsurmoto Mamoru
Input Variable	Outdoor Conditions	Temperature (℃)	O	O	O
		Relative Humidity (%)	O	O	O
		Weather data (Solar radiation etc)	-	O	O
	Indoor Conditions	Temperature (℃)	O	O	O
		Relative Humidity (%)	O	O	O
		Air change rate per time (1/h)	-	O	O
	Material property	Thermal Conductivity (W/mK)	O	O	O
		Water vapor conductivity (kg/msPa)	-	O	O
		Thermal resistance (m²K/W)	O	O	O
		Air layer thickness (m²)	O	O	O
		Water contents (kg/m³)	-	O	O
		Liquid transport coeffcient	-	O	O
		Porosity (m³/m³)	-	O	O
	Surface Coefficient	Surface heat transfer coefficient	O	O	O
	Surface Coefficient	Surface water vapour transfer conditions	-	O	O
Output Variable		Temperature (℃)	O	O	O
		Relative Humidity (%)	O	O	O
		Moisture content (kg/m³)	-	O	O

ISO 13788은 정상해석 방법으로 월평균 실내외 온습도를 기준으로 해석이 이루어지며, 열전도율, 수증기압, 열저항, 공기층 두께의 인자가 요구된다. 이는 외부 물체의 야간(장파)복사와 일사(단파장 복사)를 고려하지 않은 경계조건과, 구조체 내부축열 및 함수율에 따른 열 및 수분이동이 고려되지 않은 1차원 정상상태의 해석이어서, 실제 현상과 상이하게 과도한 결로수량이 산출되는 경향이 있다.

반면에 단순 실내외 온습도를 고려하는 ISO 13788에 비해 Matsumoto Mamoru 기반 기초방정식과 EN 15026은 기상데이터를 활용하고 구조체 내부의 시간별 축열 및 함수율의 변화를 해석할 수 있는데, 두 기초 방정식의 해석에 필요한 입력 변수 및 해석 결과는 Table 1과 같다.

EN 15026과 Matsumoto Mamoru에 기반을 둔 기초방정식의 인자들은 온도, 밀도, 비열, 열전도율 등과 같이 같은 인자들을 사용하여 서로 상호변환이 가능하며, 시간에 따른 온도, 습도, 함수율 출력이 이뤄진다. EN 15026과 Matsumoto Mamoru에 기반을 둔 기초방정식의 사용 인자는 같지만, 기초 방정식의 구동력과 확산계수를 나타내는 부분에서 차이가 있으며 내용은 다음과 같다.

EN 15026은 수분 이동의 구동력을 수증기압 $p_{v}$ 과 주변 공기의 압력 차이에 의한 모세관현상으로 기체상태와 액체상태의 수분이동이 일어나고, Matsumoto Mamoru에 기반을 둔 기초방정식은 수분의 화학포텐셜 $μ$ 을 이용하여 열 및 수분 이동의 기초방정식을 나타내고 있다.

EN 15026의 확산계수는 식 (9)와 같이 수분의 상태(기체, 액체)에 관해서 기술하고 있는 반면에, Matsumoto Mamoru의 기초방정식은 유출입 되는 수분류로 수분의 화학포텐셜 구배에 의한 수분이동( $λ'_{μ} \partial μ / \partial x$ )과 온도 구배에 의한 수분 이동( $λ'_{T} \partial T / \partial x$ )으로 식 (13), 식 (14)와 같이 구분하여 기술하고 있다. 이는, Matsumoto Mamoru의 기초방정식이 수분의 이동을 수분의 화학포텐셜 구배와 온도 구배에 따른 영향까지 고려한 반면, EN15026의 기초방정식은 수분의 이동을 온도에 의한 영향은 미비하여 고려하지 않고 다만, 수분의 상태의 영향만 기술하였다고 표현할 수 있다. 물론 EN15026 기초방정식의 수분 구동력( $p_{v}$ , $p_{s u c}$ )이 온도와 수분 포텐셜(함수율, 상대습도, 절대습도 등)에 관한 함수이므로, 이를 편미분할 때 온도의 영향도 고려해서 해석한다면 Matsumoto Mamoru에 기반을 둔 기초방정식과 유사하게 열 및 수분 이동 현상을 설명하고 있다고 볼 수 있다.

EN 15026 (Annex : Benchmark Test)

개요

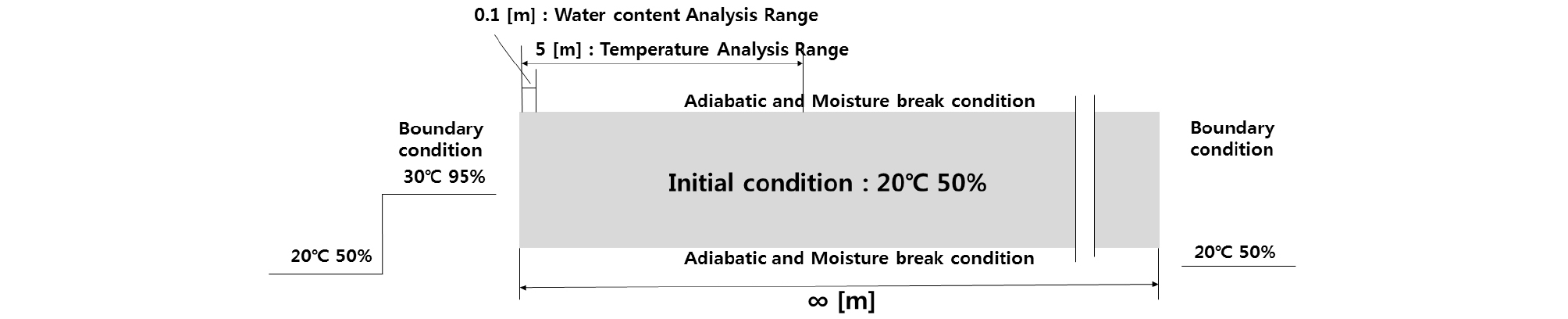
EN 15026은 내부결로 평가를 위하여 개발된 소프트웨어가 기본 요구사항을 충족하고 지정된 허용오차 내에서 정확한 결과를 제공하도록 Benchmark Test(이하 BMT라 기술함)를 정의하고 있으며, 테스트 결과는 반 무한 영역에서 열과 수분의 흐름이 결합된 해석 방법을 기반으로 한다. 분석의 계산 조건 및 판단 기준은 반 무한 영역의 단일 재료(Figure 1)를 대상으로, 초기 조건 20℃, 50%에서 30℃, 95%의 외부 온습도의 변화가 있을 경우 재료 내부의 온도 및 함수율 분포가 지정된 시간(계산 개시 후 7일, 30일, 365일째 되는 날)에서 허용범위 ±2.5%의 만족 여부를 검토하는 것이다. 단, 외적인 변화가 발생하는 경계면의 열/수분 전달저항 및 비(rain)의 영향은 고려하지 않으며, 함수율( $ρ_{w} ϕ = f_{1} (h)$ )은 습도에 관한 함수로, 수분전도율( $λ' = f_{2} (ρ_{w} ϕ)$ ), 열전도율( $λ = f_{3} (ρ_{w} ϕ)$ ), 액상 수분의 확산계수( $K = f_{4} (ρ_{w} ϕ)$ )는 모두 함수율에 관한 함수로 제시하고 있다.

http://static.apub.kr/journalsite/sites/kiaebs/2020-014-01/N0280140113/images/Figure_KIAEBS_14_1_13_F1.jpg

Figure 1.

Test scheme

Benchmark Test 수행결과

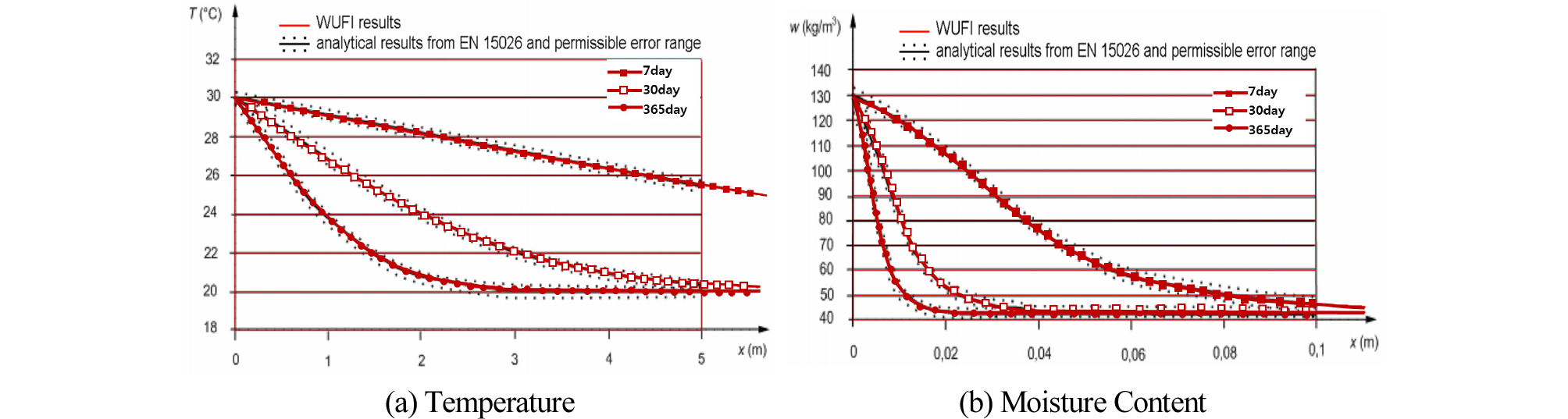
본 연구를 통해 조사된 EN 15026과 Matsumoto Mamoru에 기반을 둔 기초방정식의 오차를 비교·분석하기 위해 EN 15026에서 제시하는 BMT를 수행하였다. 먼저 EN15026에 근거한 타 사용프로그램(독일IBP Fraunhofer의 WUFI 프로그램(Fraunhofer(IBF), 2015))의 BMT결과를 살펴보면, 평가지표(오차 ±2.5%이내)를 만족하는 것으로 보고되었고, 그에 대한 결과는 Figure 2와 같다.

http://static.apub.kr/journalsite/sites/kiaebs/2020-014-01/N0280140113/images/Figure_KIAEBS_14_1_13_F2.jpg

Figure 2.

Output graph given in WUFI

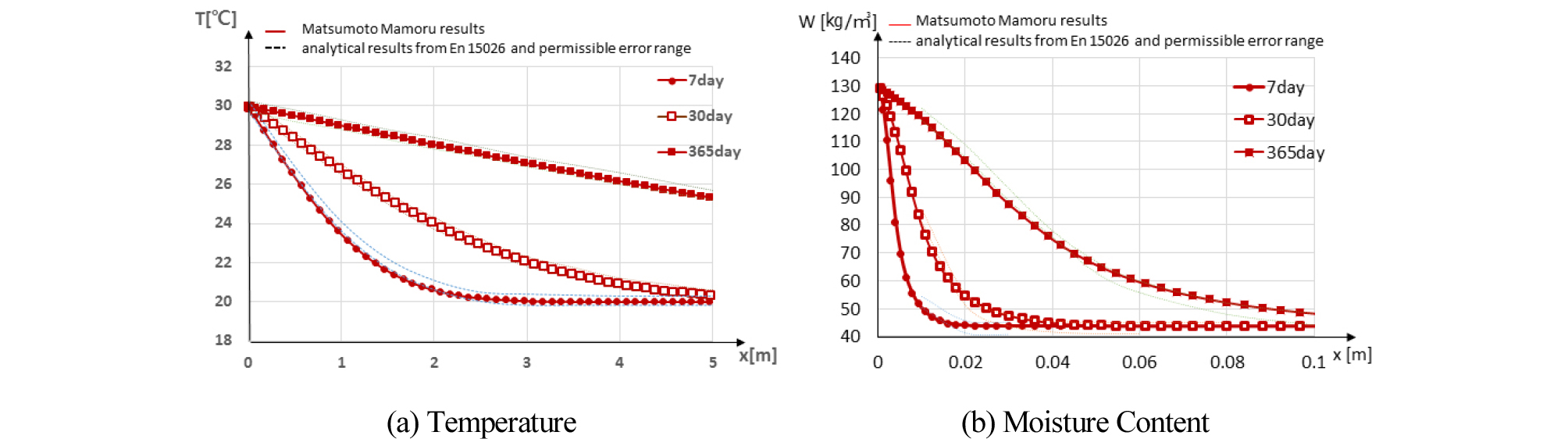
다음으로, Matsumoto Mamoru에 기반을 둔 기초방정식으로 BMT를 진행하였으며 정량적인 해석 결과는 다음 Figure 3, Table 2와 Table 3과 같다. BMT 기준과 Matsumoto Mamoru에 기반을 둔 기초방정식의 해석 결과를 비교할 시, 대부분 구간에서 만족하는 결과가 산출되었으나, 온도 분포는 3 m 지점에서 –0.03℃ (0.13% over), 함수율 분포는 0.02 m, 0.03 m 지점에서 –1.28%, -1.16% (1.3~1.32% over)의 오차가 발생하였다. 이에 대한 원인으로 1) 포화 수증기압 곡선, 2) 확산계수에 의한 차이에서 발생된 것으로 추정된다.

http://static.apub.kr/journalsite/sites/kiaebs/2020-014-01/N0280140113/images/Figure_KIAEBS_14_1_13_F3.jpg

Figure 3.

Output graph given in Developed equation

Table 2. The limits of validity for result from the temperature calculations and result of developed equation (Unit : Temperature ℃)

	Days	x = 0.5	x = 1.0	x = 1.5	x = 2.0	x = 2.5	x = 3.0	x = 4.0	x = 5.0
EN. min	7	26.40	23.60	21.70	20.60	20.00	19.80	19.80	19.80
Matsumoto Mamoru		26.61	23.62	21.67	20.65	20.16	20.07	20.00	20.00
EN. max		26.90	24.10	22.20	21.10	20.50	20.40	20.30	20.30
error		-	-	-0.03	-	-	-	-	-
EN. min	30	28.10	26.50	25.00	23.70	22.70	21.80	20.70	20.10
Matsumoto Mamoru		28.46	26.86	25.38	24.09	22.81	21.98	20.88	20.34
EN. max		28.60	27.00	25.50	24.30	23.20	22.30	21.20	20.60
error		-	-	-	-	-	-	-	-
EN. min	365	29.20	28.80	28.30	27.80	27.40	26.90	26.00	25.20
Matsumoto Mamoru		29.55	29.05	28.56	28.07	27.50	27.03	26.11	25.25
EN. max		29.80	29.30	28.80	28.40	27.90	27.40	26.60	25.70
error		-	-	-	-	-	-	-	-

Table 3. The limits of validity for result from the Water content calculations and result of developed equation (Unit : Water content kg/㎥)

	Days	x = 0.01	x = 0.02	x = 0.03	x = 0.04	x = 0.05	x = 0.06	x = 0.08	x = 0.10
EN. min	7	50.20	41.30	40.80	-
Matsumoto Mamoru		51.67	44.00	43.74
EN. max		54.50	45.60	45.10
erro		-	-	-
EN. min	30	81.00	51.10	43.60	41.50	40.90	40.90	40.80	-
Matsumoto Mamoru		83.91	52.43	46.52	44.66	43.99	43.79	43.79
EN. max		85.30	55.30	47.90	45.70	45.20	45.10	45.10
error		-	-	-	-	-	-	-
EN. min	365	117.50	104.40	88.70	75.60	62.80	55.70	47.90	44.10
Matsumoto Mamoru		119.38	103.02	87.54	76.01	64.91	59.02	50.38	47.04
EN. max		121.80	108.70	93.00	77.90	67.10	60.00	52.20	48.40
error		-	-1.38	-1.16	-	-	-	-	-

첫 번째 원인으로 추정되는 포화수증기압은 온도에 관한 함수로 기초방정식에서 보는 바와 같이 열 및 수분의 포텐셜과 확산계수 모두에 영향을 미치는 변수이다. Matsumoto Mamoru에 기반을 둔 기초방정식은 SONTAG의 식(JIS Z8806, 1995)을 사용하여 포화수증기압을 계산하였는데, EN 15026은 별도로 제시된 함수가 없으므로 오차의 원인으로 사료된다.

두 번째 원인으로 추정되는 확산계수는 온도의 의존성을 고려하는 것에 따라 차이가 발생된다. Matsumoto Mamoru에 기반을 둔 기초방정식은 수분의 화학포텐셜 구배에 의한 수분이동( $λ'_{μ} \partial μ / \partial x$ )과, 온도 구배에 의한 수분이동( $λ'_{T} \partial T / \partial x$ )으로 구분하여 기술하고 있지만, EN의 기초방정식에는 온도에 대한 영향은 고려하지 않고 있어 이 차이가 결과값에 영향이 미치는 것으로 사료된다.

결 론

본 논문은 국내 내부결로 판단 기준 정립 및 방법론 구축을 위하여 국외의 ISO 13788, EN 15026, Matsumoto Mamoru 식에 체계화된 열·습기 거동 기초방정식을 조사하고, 각 기준별 해석방법에 대한 차이를 비교·분석하고자 EN 15026 Benchmark Test를 수행하였으며, 주요 결과는 다음과 같다.

(1)국외 내부결로 평가 기준을 비교한 결과, ISO 13788은 수증기 압차에 의한 정상상태 해석으로 결로량이 산출되며, 시간 변화에 따른 결로량을 확인하는 것에 한계가 있고, EN 15026과 Matsumoto Mamoru 기반의 열 및 수분 이동방정식은 비정상 해석으로 기후데이터를 반영한 해석이 가능하며, 특정 시간에 대한 결로량을 확인할 수 있는 것으로 조사되었다.

(2)이에, 열·습기 거동 기초방정식이 EN 15026과 Matsumoto Mamoru가 유사한 것으로 분석되었으며, 사용된 인자들이 서로 상호 적용이 가능하나 기초방정식의 구동력과 확산계수를 산출하는 방식에서 차이가 있음을 확인하였다.

(3)이에, EN 15026 기준에서 제시하고 있는 Benchmark Test를 진행한 결과, EN 15026과 Matsumoto Mamoru 식 기반의 열 및 수분 이동방정식의 전체적인 분포 및 그래프의 형상은 매우 유사한 것으로 확인되었으며, 오차(온도 0.03%, 함습량 1.38%)의 원인은 수분 이동의 구동력과 확산계수에 의한 차이로 사료된다.

이상의 과정을 통해, 본 연구는 국외에서 사용되는 내부결로 평가방법을 조사 및 비교 분석하여, Matsumoto가 제안한 비정상 열 및 수분 동시 이동 방정식의 적합성을 검증하였다.

본 연구에서 사용한 Matsumoto 기초방정식은 열 및 수분이 동시 이동할 경우, 온도 구배에 의한 수분이동까지 고려하여 해석할 수 있어, 연간 벽체 내부 온습도 상태를 다른 평가방법보다 더 정확하게 해석할 수 있을 것으로 사료된다. 이에, 본 연구는 추후 내부결로를 평가할 수 있는 간이 해석프로그램을 개발하고, 이를 토대로 국내 내부결로 판단기준 수립 및 결로에 의한 피해 방지를 위한 설계 및 시공 가이드라인을 작성 및 보급하고자 한다.

Acknowledgements

이 논문은 2019년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원(No. 2017R1C1B2008728)을 받아 수행된 연구임.

References

Hong, S.-W., Kang, H.-S., Park, C.-Y., Jang, H.-I. (2017). A Study on the Effect of Material Properties Related to Liquid Transport on the Maximum Cumulative Condensation, Journal of KIAEBS, 11(6), 572-585.

10.12972/jkiaebs.20170026

Kim, K.-S., Jang, H.-I., Park, C.-Y., Yoo, D.-C., Choi, C.-H. (2017). Comparison of Total Moisture Content by Internal Condensation Evaluation Method, Journal of KIAEBS, 11(6), 558-571.

10.12972/jkiaebs.20170025

Ministry of Land, Infrastructure and Transport. (2016). Design Criteria for Preventing Condensation in Apartment Houses.

New Architecture Department Editorial Board 10 Environmental physics. (1984). Matsumoto Mamoru, Syokokusya Co. ltd., pp. 105-132.

EN 15026. (2007). Hygrothermal Performance of Building Components and Building Elements. Assessment of moisture transfer by numerical simulation.

Fraunhofer (IBF). (2015). WUFI Passes Benchmark Test of EN 15026.

ISO 13788. (2007). Hygrothermal performance of building components and building element -Internal surface temperature to avoid critical surface humidity and interstitial condensation- Calculation methods.

JIS-Z-8806. (1995). Humidity - Measurement Methods.

Journal of Korean Institute of Architectural Sustainable Environment and Building Systems ISSN:1976-6483(Print) 2586-0666(Online) 한국건축친환경설비학회논문집

Preview

Result Comparison of Internal Condensation Evaluation method through EN 15026 Benchmark Test

ABSTRACT

MAIN

Figure 1.

Figure 2.

Figure 3.

Acknowledgements

References