서 론
CFD 모델의 적정 격자 수 관련 선행 연구 분석
격자 해상도를 반영한 격자 독립성 검정 방법
CFD에 적합한 격자 해상도 반영 방법
격자 해상도를 적용한 개선된 격자 독립성 검정 방법
개선된 격자 독립성 검정을 이용한 적정 격자 해상도 평가
대상 시설 선정
CFD 모델 설계 및 적정 해상도 평가 방법
격자 해상도별 CFD 모델 설계 결과
적정 격자 해상도 평가 결과
결 론
서 론
전산유체역학(Computational Fluid Dynamics, CFD)은 수치해석을 통해 유체의 흐름을 해석하는 도구이다. 건설산업에서 CFD는 환기 평가, 온열 환경 평가, 오염 확산 분석 등 유체에 대한 3차원 분석이 필요한 다양한 연구 분야에 활용되고 있다(Kato, 2018; Zhang et al., 2019). CFD로 물리적 현상을 해석하기 위해서는 격자 설계를 통해 먼저 분석 대상 공간을 유한개의 격자로 분할해야 한다(Zhang et al., 2009). 분할된 격자를 대상으로 물리적 현상을 해석하기 때문에 격자 분할 결과에 따라 근사해의 정확성이 달라지며, 결과적으로 전체 해석 결과에 큰 영향을 미친다(Shepherd and Johnnson, 2008). 이에 따라, CFD 모델에 대한 최적 격자 설계를 통해 CFD 시뮬레이션 분석의 정확도를 향상시킬 수 있다.
CFD 모델의 최적 격자 설계를 위한 적정 격자 수 또는 최소 격자 크기는 격자 독립성 검정을 통해 결정된다. 격자 독립성 검정은 검정을 수행할 격자 후보 조건을 선정하고, 격자 조건별로 CFD 모델을 설계한 후 시뮬레이션을 수행하는 과정으로 이루어진다(Chaube et al., 2006; Fernande et al., 2007; Boulard et al., 2010; Hong et al., 2011, Hong et al., 2015; Kwon et al., 2016). 이후 최적 격자 판단을 위하여 최소 격자 크기 또는 최대 격자 수 조건의 연산 결과를 기준으로 각 격자 조건에 대한 연산 결과를 비교한다. 마지막으로 연산 결과 비교를 통해 격자 조건에 대하여 독립성을 확보하는 격자 조건을 판단하고 이를 최적 격자 조건으로 정의한다. 현재 국내에는 이와 같은 격자 독립성 검정 과정에서 격자 후보의 선정에 대한 명확한 기준이나 근거가 없어 대부분 연구자가 임의로 격자 후보를 선정하고 있다. 이로 인해 적정 격자 조건을 포함하지 않은 격자 후보군이 선정되거나, 연구자의 의도를 반영한 격자 후보군 선정 등 부적절한 격자 후보 선정이 이루어질 수 있다. 또한, 같은 분석 조건 및 대상에서도 연구자별로 서로 다른 격자 후보가 선정되거나, CFD 분석 모델에 적절하지 않은 격자 조건을 도출하는 문제가 발생할 수 있다. 특히, 건물의 경우에 분석 대상의 규모가 일정하지 않을 뿐만 아니라 차이도 크기 때문에 개인의 주관적 판단에 의한 격자 후보 선정 문제가 심화되고 있다.
본 연구에서는 연구자의 주관적 판단에 의존하는 기존 격자 독립성 검정 방법을 개선하기 위하여 격자 해상도를 적용한 새로운 격자 독립성 검정 방법을 제안하였다. 화재 시뮬레이션 분야에 적용되던 격자 해상도의 CFD 분석 적용 가능성을 확인하고자 하였으며, 이를 통해 새로운 격자 생성 가이드라인 방향을 제시하고자 하였다. 이를 위해, 기존 격자 독립성 검정 방법에 특성길이, 격자 해상도를 반영하는 개선된 독립성 검정 방법을 제안하였다. 이와 함께, 본 연구에서 제안한 독립성 검정 방법의 적합성을 평가하기 위해 파일럿 테스트를 수행하였다. 파일럿 테스트는 우선적으로 기존 선행 연구를 통해 도출된 적정 격자 해상도 범위에 대해서만 진행하였다. 임의의 실내 건축물 형상과 난류 모델에 대하여 독립성 검정으로 도출된 적정 격자 해상도와 CFD 시뮬레이션의 기류 분포 분석을 수행하였다.
CFD 모델의 적정 격자 수 관련 선행 연구 분석
국외에서는 적정 격자 수 또는 격자 크기와 관련한 권장 기준이 존재한다. 일본건축학회(Architectural Institute of Japan, AIJ) 가이드라인에서는 격자 크기를 건물 규모(대략 0.5-5.0 m로 가정함)의 약 10%로 설정할 것을 권장하고 있다(Tominaga et al., 2008). 해당 가이드라인에서는 평가 대상 높이(약 1.5-5.0 m)를 포함한 격자는 지표면으로부터 3번째로 높은 격자가 되도록 설계할 것을 권장하고 있다(Yoshie et al., 2005; Tominaga et al., 2005). 유럽과학기술연구협력(European Cooperation in Science and Technology, COST)은 대상 건물 체적의 세제곱근에 해당하는 부피와 건물 주변 영역에 최소 10개 이상의 격자가 설계될 것을 권장하고 있다. 또한 AIJ 가이드라인과 유사하게 1.5-2 m 높이의 격자가 지표면으로부터 3번째 순서의 격자가 되도록 설계할 것을 권장하고 있다(Franke et al., 2004). 이처럼 국외에서는 건물 외부에 형성되는 풍환경 분석을 주요 대상으로 설정하고, 건물의 규모에 따라 적정 격자 수 또는 크기와 관련한 기준을 제시하고 있다. 외부 기류 분석의 경우, 연산 영역 크기가 방대하기 때문에 두 가이드라인에서 제시하고 있는 격자 크기도 충분한 조밀도를 확보할 수 있다. 그러나, 이에 비해 연산 영역이 작고 복잡한 형상이 포함된 실내 기류 분석에 있어서는 두 가이드라인이 제시하는 격자 크기는 충분한 조밀도를 확보가 어렵기 때문에, 실내 환기, 온열 환경 분석을 위한 CFD 모델에는 적합성이 저하된다.
건물의 실내 공간을 대상으로 적정 격자 수 또는 크기를 제시한 CFD 관련 기준의 개발은 현재까지 미흡한 실정이다. 다만, 화재 시뮬레이션(Fire Dynamic Simulator, FDS) 분야의 경우에 실내 공간의 적정 격자와 관련하여 미국 원자력 규제위원회에서 발간한 관련 가이드라인인 NUREG-1824에서 격자 해상도 개념을 이용하여 적정 격자 조밀도를 제시하고 있다. 격자 조밀도는 실내 공간의 화재 확산에 대한 특성길이를 최소 격자 크기로 나눈 값으로 4-16에 해당하는 해상도를 적정 해상도로 권장하고 있다(Sally and Lindeman, 2016). FDS 역시 수치해석에 기반을 둔 시뮬레이션이므로, 수치해석에 기반을 둔 CFD 시뮬레이션의 적정 격자 수 혹은 최소 격자 크기 설정에 격자 해상도를 적용할 수 있을 것으로 판단된다. 그러나 FDS 분야에서의 격자 해상도는 화재 확산의 특성길이를 이용하여 정의하고 있으므로 이를 건축물 기류 분석에 적용하는 것은 타당하지 않으며, CFD에 적합하게 수정이 필요하다.
격자 해상도를 반영한 격자 독립성 검정 방법
CFD에 적합한 격자 해상도 반영 방법
격자 해상도는 NUREG-1824에서 제시하고 있는 적정 격자 개념으로 격자의 상대적인 조밀도를 나타내는 무차원 지표이다. 체적에 대한 격자의 수로 계산되는 일반적인 조밀도와 달리 격자 해상도는 식 (1)과 같이 화재의 확산에 대한 특성길이에 대한 미소 격자의 크기의 비로 정의된다.
| $$R=\frac{D\ast}{max(\delta x,\;\delta y,\;\delta z)}$$ | (1) |
여기서, 은 격자 해상도, 은 화재 특성길이(m), 미소 격자의 대표 크기(m)이다.
화재 특성길이(Characteristic diameter)는 주변 변인들에 대한 화재의 확산 특성을 나타내는 개념이다(Wang et al., 2016). 격자 해상도는 식 (1)과 같이 시뮬레이션의 주요 해석 대상이 되는 화재의 확산을 표현하는 특성길이를 미소격자 크기로 나누어 해상도를 계산한다.
한편, 기존 격자 해상도는 화재 확산 분석을 위한 시뮬레이션에 적용된 개념이므로, 이를 기류 분석을 위한 CFD에 적합하도록 수정하였다. 기존 식 (1)의 화재 확산에 대한 특성길이를 CFD 분석의 주요 대상인 기체 즉 유체의 확산에 대한 특성길이로 대치하고자 하였다. 유체의 특성길이는 유동의 흐름 특성(난류, 층류)을 판별하기 위하여 사용되는 레이놀즈 수(Reynolds number) 계산에 사용되는 개념으로 아래 식 (2)와 같이 적용된다.
| $$Re=\frac{\rho vD}\mu$$ | (2) |
여기서, 는 레이놀즈 수, 는 유체의 밀도(), 는 유체의 속력(), 는 유체역학적 특성길이(), 는 유체의 점성계수()이다.
유체역학적 특성길이는 원형관을 흐르는 유체일 경우 관의 내경을 특성길이로 정의 가능하며, 원형이 아닌 관을 흐르는 경우 수력학적 직경(Hydraulic diameter)으로 값으로 정의한다. CFD의 주요 매개체인공기 역시 유체이며 기류가 흐르는 실내 공간을 하나의 관 시스템으로 정의 가능하므로 건축물에 대해서도 특성 길이 계산이 가능하다. 따라서, 본 연구에서 사용한 유체역학적 특성길이는 아래 식 (3)과 같이 계산된다.
| $$D=\frac VA$$ | (3) |
여기서, 는 분석 대상의 체적(), 는 분석 대상의 표면적()이다.
화재 확산에 대한 특성을 나타내는 화재 특성길이와 동일하게 유체 특성길이는 유체 흐름에 대한 특성을 표현하며, 길이 차원으로 표현된다. 두 특성길이 모두 분석 대상에 대한 확산의 특성을 나타내는 개념이므로 CFD 분석에 있어서는 식 (1)의 화재 특성길이를 유체역학적 특성길이로 대체가 가능하다. 따라서, 화재 특성길이 대신 해상도 계산 및 격자 독립성 검정에 적용하여 건축물 형상이 기류에 미치는 영향을 반영하였으며 최종적으로 격자 해상도를 식 (4)와 같이 수정하였다.
| $$R\ast=\frac D{max(\delta x,\;\delta y,\;\delta z)}$$ | (4) |
여기서, 은 수정 격자 해상도이다.
격자 해상도를 적용한 개선된 격자 독립성 검정 방법
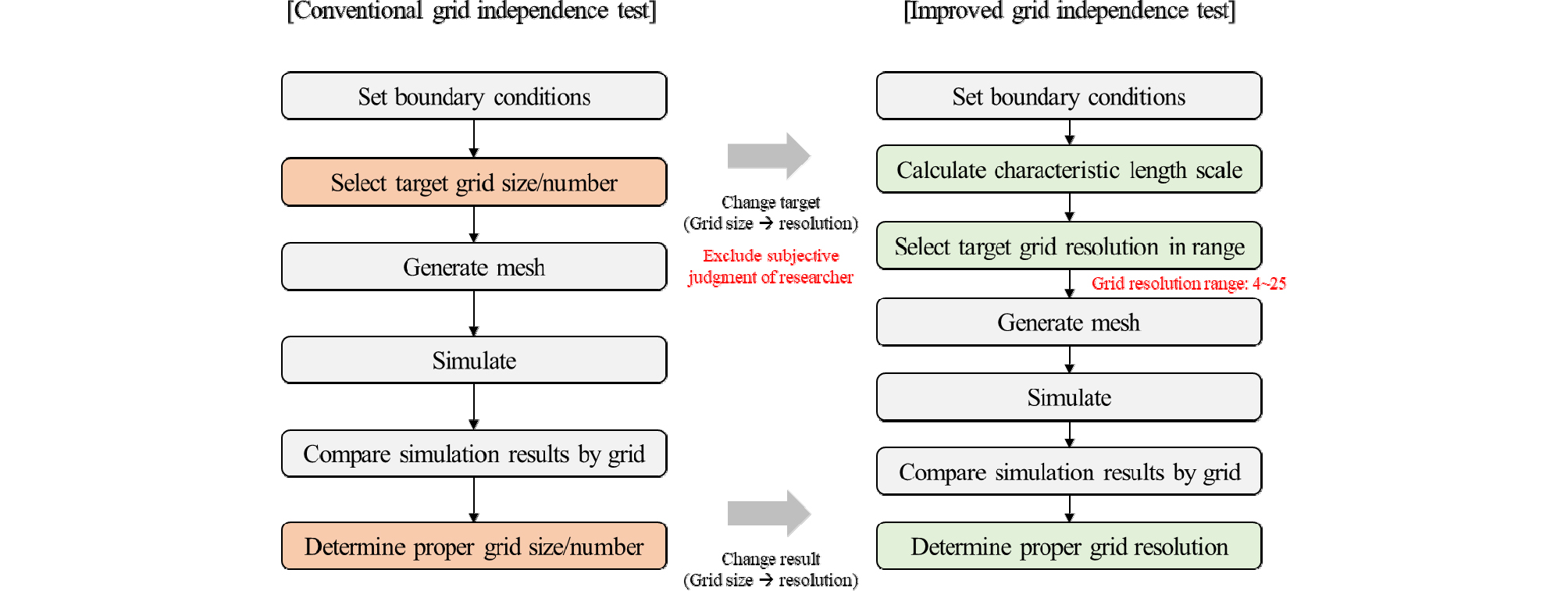
기존 격자 독립성 검정 방법에 격자 해상도와 특성길이를 반영하여 Figure 1과 같이 개선된 격자 독립성 검정 방법을 도출하였다. 본 연구에서 제안하는 개선된 격자 독립성 검정은 경계조건 설정 이후, 건축물 형상에 대한 특성길이를 우선적으로 산정한다. 이후 격자 독립성 검정을 위한 격자 후보 선정을 수행한다.
격자 후보 선정에 대한 주관적인 판단 개입의 배제와 객관성 확보를 위하여 적정 값에 대한 규정이 어려운 최소 격자 크기나 격자 수 대신 격자 해상도를 선정하는 것으로 수정하였다. 한편, 기존 선행 연구 분석을 통하여 시뮬레이션에 적합한 격자 해상도 범위가 4-25로 도출되었다(Kim and Lee, 2008; Hassanien et al., 2017). 이를 격자 후보로 정의하고 이에 대한 독립성 검정을 수행하도록 하였다. 도출된 격자 해상도를 앞서 계산한 특성길이로 나누고 역수를 취하면 해당 CFD 모델의 최소 격자 크기를 산정할 수 있다. 이를 통해 각 해상도별 CFD 모델의 격자를 설계하고 검정을 수행한다. 최종적으로, 독립성 검정의 최종 결과로 최소 격자 크기가 아닌 적정 격자 해상도를 도출하도록 수정하였다.
개선된 격자 독립성 검정을 이용한 적정 격자 해상도 평가
본 연구에서 제안한 격자 독립성 검정 방법의 적합성을 평가하기 위하여 파일럿 테스트를 수행하였다. 독립성 검정으로 도출된 적정 격자 해상도와 실제 시뮬레이션의 기류 분포를 비교하여 개선된 독립성 검정이 적합하게 격자 해상도를 판단하는지 검증하였다.
대상 시설 선정
실내 기류 분석을 위한 파일럿 테스트 대상 시설은 Figure 2와 같이 3가지의 건축물 실내 형상을 선정하였다. 실내의 바닥면적 및 부피에 따라 형성되는 기류 또한 영향을 받을 수 있으므로, 바닥면적이 넓은 Shape 1과 바닥면적이 작은 Shape 2에 대해 적합성을 평가하고자 하였다. 이와 함께 실내 형상의 배치와 복잡성에 따라 기류 형성이 달라지므로, 형상이 복잡한 Shape 2와 상대적으로 형상이 단순한 Shape 3에 대해서도 적합성 평가를 수행하였다. 각 대상별 규격, 특성길이에 대한 상세 정보는 Table 1과 같다. Figure 2의 각 대상 시설별로 청색면은 대상 시설의 유입구이며, 적색면은 유출구이다.
Table 1. Geographical information and characteristic length of target model
| Shape_1 | Shape_2 | Shape_3 | |
| Floor area | 130.7 m2 | 49.6 m2 | 50.6 m2 |
| Height | 2.8 m | 3.3 m | 4.0 m |
| Volume | 365.9 m3 | 163.1 m3 | 202.5 m3 |
| Characteristic Length | 0.9387 | 0.8500 | 0.9325 |
CFD 모델 설계 및 적정 해상도 평가 방법
대상 시설의 격자 설계 및 시뮬레이션은 개방형 CFD 소프트웨어인 OpenFOAM을 사용하였다. 격자 설계는 cfMesh를 이용하였으며, 격자의 형상은 고품질의 격자 설계가 가능한 육면체 기반의 격자계를 구성하였다 (Hefny and Ooka, 2009). cfMesh는 Creatvie Fields 사에서 개발하여 배포하는 공개 격자 생성 도구로 육면체 격자 설계를 위하여 cartesianMesh 옵션을 적용하였다. 해당 옵션은 대상 영역에 대하여 우선적으로 육면체 격자를 설계하며, 일부 모서리 부분 등에서는 사면체를 포함한 다면체 격자계를 형성한다. 격자의 크기는 수정 격자 독립성 검정 및 해상도 평가 방법에 따라 설정하였다.
난류 모델이 독립성 검정 및 격자 해상도에 미치는 영향을 반영하고자 Standard k-ε, RNG k-ε, Realizable K-ε의 총 3가지 난류 모델을 적용하였다. 분석 대상 격자 해상도는 4-25 범위 중 총 6개(4, 8, 12, 16, 20, 24)에 대하여 독립성 검정을 수행하였다. 구체적인 분석 조건은 다음 Table 2와 같다.
Table 2. Analysis condition of CFD simulations
| Factor | Contents |
| Target shape | Shape 1, Shape 2, Shape 3 |
| Grid resolution | 4, 8, 12, 16, 20, 24 |
| Turbulence model | Standard k-ε, RNG k-ε, Realizable k-ε |
기류 분석을 위한 Solver는 비압축성 기체의 난류 해석 Sovler인 simpleFoam을 이용하여 정상상태 해석을 하였다. 각 대상시설의 유입구는 Inlet, 유출구는 Outlet, 그 외 벽체는 Wall로 경계조건을 설정하였으며, 유입구에서 1.0 m/s 풍속으로 공기가 유입된다. Inlet에서 난류 운동 에너지(k)는 유입 풍속과 난류 강도를 고려하여 3.75e-3 m3/m2로 동일하게 적용하였다. 그 외 경계 조건은 Table 3과 같다.
Table 3. Boundary condition types of target CFD models
적정 격자 해상도를 평가를 위하여, 각 CFD 모델의 정상상태 해석을 수행한 후, 0.1 m 간격으로 유속 값을 추출하였다. 가장 조밀한 격자 조건인 해상도 24인 조건을 기준으로 유속 연산 결과의 결정 계수(R2)와 상대 오차율을 분석하였다. 적정 격자 해상도 판별 기준은 R2 0.95 이상, 상대 오차율 5%이하로 적용하여 해당 기준을 충족하는 해상도를 적정 격자 해상도로 도출하였다. 적정 격자 해상도 판별 기준을 충족하는 해상도가 다수일 경우, 해상도가 작은 조건을 적정으로 판별하였다.
격자 해상도별 CFD 모델 설계 결과
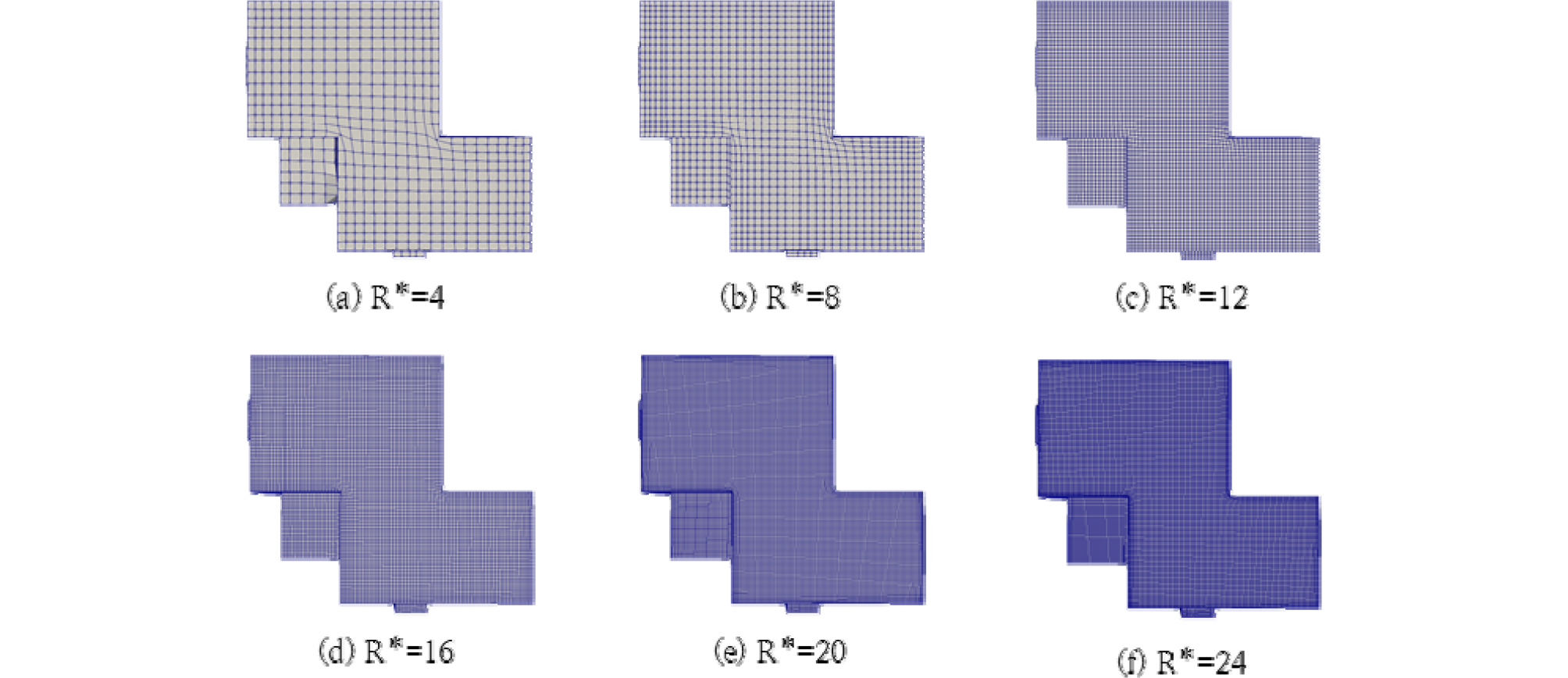
대상 시설의 특성길이를 이용하여 해상도 조건에 맞는 최소 격자 크기를 산정하였으며, 이를 이용하여 Figure 3과 같이 해상도별 CFD 모델의 격자 설계를 수행하였다. 각 해상도에 대하여 설계된 격자 수는 Table 4와 같다.
Table 4. Number of grids in each condition
적정 격자 해상도 평가 결과
개선된 격자 독립성 검정을 바탕으로 파일럿 테스트를 수행하였으며, 파일럿 테스트 결과는 Table 5, Table 6, Table 7과 같다. Shape 2의 경우 Standard k-ε 난류 모델에서는 적정 해상도 조건을 만족하는 해상도가 16, 20으로 도출되었으며, 둘 중 낮은 해상도인 16이 최적 격자 해상도로 도출되었다. Shape 3의 Standard k-ε 난류 모델 조건에서는 격자 해상도 20이 적정 해상도로 도출되었다. 그 외의 경우 상대 오차율과 R2를 만족하는 해상도가 도출되지 않아 가장 조밀한 해상도인 24가 적정 격자 해상도로 도출되었다.
Table 5. Result of gird independence test (Shape 1)
Table 6. Result of gird independence test (Shape 2)
Table 7. Result of gird independence test (Shape 3)
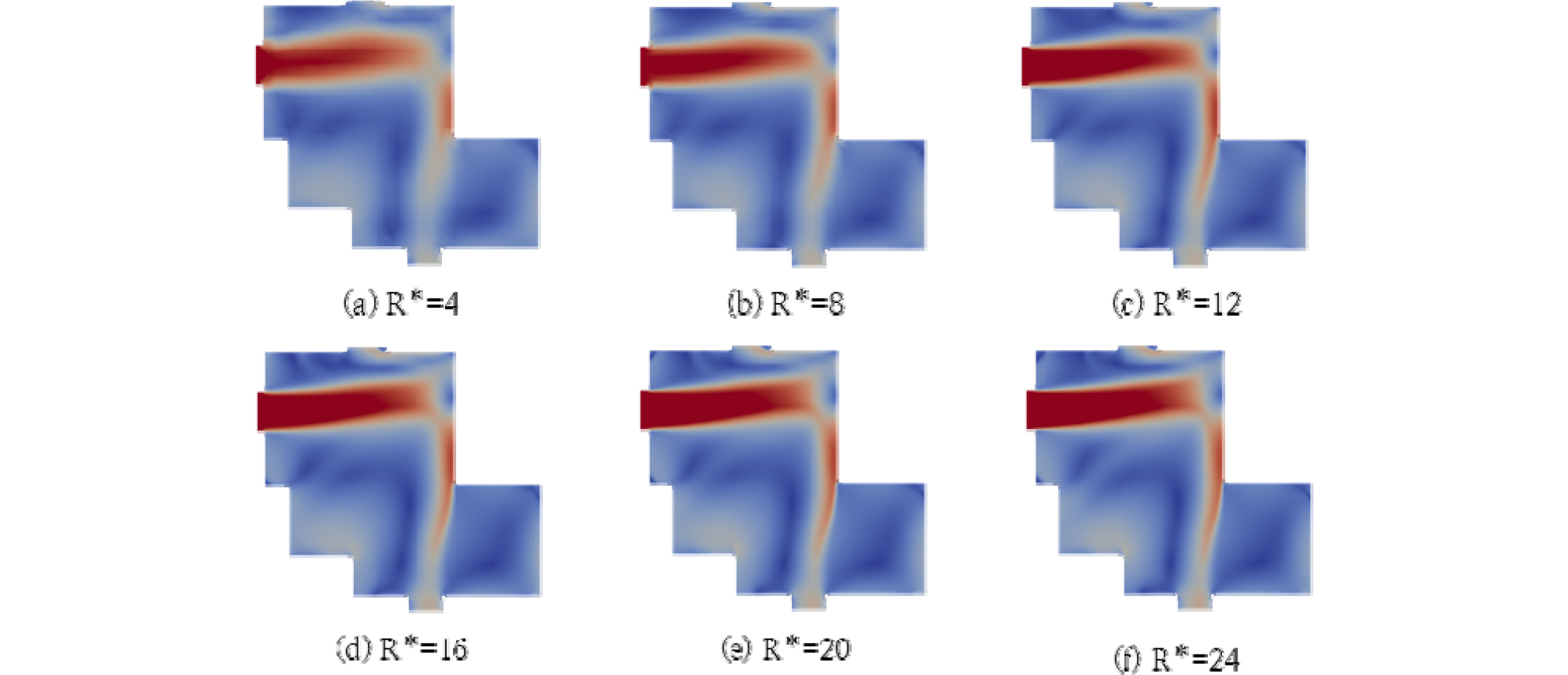
Figure 4는 Shape 2의 Standard k-ε난류 모델 조건일 때, 각 격자 해상도 CFD 모델에서 1.0 m 높이의 유속 분포를 나타낸 결과이다. 해상도가 가장 높은 (f)와 해상도 16, 20 조건의 유속 분포는 정성적으로 차이가 발생하지 않았다. 반면, 해상도가 가장 낮은 (a), (b)의 경우 유입 기류 분포가 확연하게 차이가 발생함을 알 수 있다. 즉, 격자가 조밀하지 못한 (a), (b)의 경우 유입 기류를 정밀하게 해석하지 못하여 유속 분포에 차이가 발생하였으며 이로 인하여 Table 6과 같이 상대 오차율 및 R2 차이가 발생함을 알 수 있다. 따라서, 개선된 격자 독립성 검정 방법이 실제 기류 분포에 잘 부합하게 적정 격자 해상도를 도출한다고 판단 가능하다.
최종적으로, 분석 조건들에 대하여 최적 격자 해상도를 정리한 결과는 Table 8과 같다. Shape 2의 Standard k-ε과 Shape 3의 Standard k-ε조건을 제외한 나머지 조건에서는 해상도 24가 적정 격자 해상도로 도출되었다. 대다수의 조건에서 적정 격자 해상도가 24로 도출되어 보편적으로 적용 가능한 적정 격자 해상도를 24로 유추 가능하나 이에 대한 신뢰성 확보를 위해서는 추후 지속적인 연구가 필요할 것으로 판단된다.
Table 8. Analysis result of optimal grid resolution
결 론
본 연구에서는 CFD 시뮬레이션 모델의 최적 격자 선정 방법에 대한 새로운 가이드라인을 제시하고자 격자 해상도를 이용한 격자 독립성 검정 방법을 제안하였다. 기존 격자 독립성 검정은 격자 후보 선정에 기준이 존재하지 않아, 연구자의 주관적인 판단에 격자 후보 선정을 진행하던 한계가 존재하였다. 본 연구에서는 격자 해상도 개념을 독립성 검정에 적용하여, 객관적으로 격자 후보 범위를 설정하고자 하였다. 또한, 화재 시뮬레이션에 대한 기존 격자 해상도를 적용하기 위하여 화재 특성길이 대신 유체 특성길이를 격자 해상도 산정에 적용하였다.
개선된 격자 독립성 검정의 적합성 평가를 위하여 파일럿 테스트를 실시하였다. 3개의 건물 형상에 대하여 3개의 난류 모델, 6개의 격자 해상도를 적용하여 독립성 평가를 수행하였다. 독립성 평가 결과, 실제 기류 분포의 변화를 고려한 적정 격자 해상도를 도출하여 실제 CFD 분석 적용에 적합한 것으로 판단되었다. 파일럿 테스트 중 대다수의 조건에서 적정 해상도로 24가 도출되었다. 이러한 결과를 바탕으로, 실내 기류 분석에 적합한 CFD 모델의 적정 격자 해상도가 24임을 유추할 수 있다. 적합성 평가는 동일 격자 간격을 적용한 CFD 모델에 대해서 적정 격자 해상도를 도출하였으나, 격자 조밀도를 부분별로 조정이 필요한 복잡한 CFD 모델에 대해서도 기준이 되는 적합한 격자 크기 선정에 본 연구의 방법을 활용 가능하다.
본 연구에서는 화재 시뮬레이션 분야에 사용되는 격자 해상도의 CFD 분석 적용 가능성을 확인하고, 새로운 방향을 제시하고자 하였다. 따라서, 선행 연구의 적정 격자 범위에 대해서 우선적으로 적합성 평가를 수행하였으며 그 결과, 적정 해상도가 24로 도출되었다. 향후 연구에서는 더 다양한 실내 형상과 24 이상의 해상도에 조건에 대한 분석을 추가로 진행하여 적정 격자 해상도에 대한 신뢰성을 향상하고자 한다.