서 론
기존 지중 열교환기 설계 방법
간략 설계 방법
ASHRAE design procedure
Design tool
기존 지중 열교환기 열해석 모델
해석적 모델
응답함수 모델
수치해석 모델
지중 열교환기 등가 열해석 모델 제안
지중 열교환기 등가 열해석 모델 주요 알고리즘
지중 열교환기 등가 열해석 모델 검증
결 론
서 론
천부 지열을 이용한 지열 히트펌프 시스템은 온실가스 감축을 위해 건물 단위에서 활용할 수 있는 대표적인 에너지 절약적 기법이다. 지중 열교환기는 지열 히트펌프의 작동을 위한 heat source 또는 heat sink의 기능을 담당하는데 히트펌프의 안정적인 운영을 위해서는 지중 열교환기의 적절한 설계가 필수적이다. 지중 열교환기 설계 프로세스는 일반적으로 지중 열교환기에서 담당해야 하는 부하를 산정하고 이를 바탕으로 지중 온도 변화량을 계산한 뒤, 최종적으로 지중 열교환기의 길이를 결정하는 것으로 이루어진다. 대표적인 지중 열교환기 설계 방법인 ASHRAE design procedure와 GLHEpro와 같은 지열 히트펌프 전용 설계 툴에 적용된 지중 온도 변화 계산에 관한 방법론은 각기 다르지만 두 방법 모두 공통적으로 지중 열교환기에서 시간에 따라 일정한 열류가 연속적으로 지중으로 전달된다는 가정에서 지중 온도 변화를 계산하고 있다. 이러한 접근 방법은 간헐적인 운전과 같은 실질적인 지열 히트펌프의 운전 상태를 고려하기 어렵지만, 계산의 편의성을 제공한다는 측면에서 대부분의 지열 히트펌프 설계 방법에서 채택되어 왔다.
하지만, 이러한 가정에서는 지열 히트펌프의 운전이 중지되는 동안 발생하는 지중 복원력에 대한 영향을 반영하기 어렵다. Cui et al. (2008)의 연구에서는 지중 열교환기의 비연속 운전으로 인하여 지중 복원력이 향상되는 것을 확인하였고, Cao et al. (2015)의 연구를 통해서는 지열 히트펌프의 간헐 운전이 성능 향상에 기여하는 것을 확인할 수 있다. 또한, Jalaluddin and Miyara (2012)의 연구에서는 비연속 운전이 지중 열교환기의 성능 향상에 기여를 할 뿐만 아니라, 이러한 성능 향상 효과로 지중 열교환기의 길이를 줄이는 것도 가능하다는 결론을 내렸다.
본 연구는 지중 복원력을 고려한 지중 열교환기의 설계에 관한 선행 연구로써, 기존의 지중 열교환기 설계 방법과 지중 온도 열해석 모델에 관한 분석을 수행하여 기존의 방법이 지중 복원력을 고려한 설계에 적합한 지 여부를 우선적으로 판단하였다. 다음으로 지중 복원력을 고려한 지중 열교환기 열해석을 위한 등가 열해석 모델을 제안하고 실측 데이터와의 비교를 통해 검증을 수행하였다.
기존 지중 열교환기 설계 방법
간략 설계 방법
지중 열교환기 설계의 목적은 일반적으로 지중 열교환기 길이를 결정하는 것이지만, 일부 연구에서는 지중열 추출량 산정 방법을 제안하고 있다. 독일의 지열 히트펌프에 과한 설치 기준인 VDI 4640 (VDI, 2015)은 비록 30 kW이하의 소규모 용량을 대상으로 하지만, 지중의 열전도율에 따라서 지중 열교환기의 단위 길이당 지중열 추출량 데이터를 표의 형태로 제시하고 있다.
Curtis et al. (2013)의 연구에서는 GLHEpro를 이용하여 얻은 결과를 기반으로 설계 데이터를 그래프의 형태로 제시하고 있다. 본 연구에서는 다양한 설계 변수와 성능 영향 인자는 고정하고 지중 온도와 지중의 열전도율에 따른 지중 열교환기의 단위 길이당 지중열 추출량 데이터를 제시하였다. 반면에 Gultekin et al. (2014)의 연구에서는 정밀한 수치해석 모델인 COMSOL multi physics를 이용하여 동적 시뮬레이션을 수행하고 그 결과를 이용하여 운영에 따른 성능 저하 데이터를 제시하였다. 지속적인 지중열 추출에 따른 지중 온도 변화는 지중열 추출량에도 영향을 미치므로, 이러한 영향 관계를 파악하기 위한 목적으로 연구가 수행되었다. 본 연구에서는 지중 열교환기 배치를 4가지로 고정하고 지중 열교환기 사이의 거리에 따른 성능 저하율 데이터를 제시하였다.
이러한 간략 설계 방법은 도표를 이용하여 간단하게 지중 열교환기의 성능을 파악할 수 있다는 장점이 있다. 하지만, 지중열 추출에 따른 지중 온도 변화를 반영한 설계가 어려워 지중 열교환기 설계에 일반적으로 쓰이고 있지는 않고 있다. 다만, 지중 열교환기의 설계에 필요한 다양한 설계 인자의 값이 주어지지 않더라도 지중의 종류와 지역의 기후에 따라서 간략하게 지중 열교환기의 용량을 산정할 수 있어 상세 설계를 하기에 앞서 기본 설계의 단계에서 적절하게 활용될 수 있을 것으로 판단된다.
ASHRAE design procedure
ASHRAE design procedure는 Steve Kavanaugh에 의해 제안되었고, ASHRAE handbook HVAC Applications (ASHRAE, 2011)에도 수록되어 있는 방법이다. 컴퓨터 프로그램을 이용하지 않고, handbook에 제시된 데이터만을 이용하여 지중 열교환기의 설계를 수행할 수 있다. ASHRAE design procedure는 앞서 살펴본 간략 설계 방법과 달리 주어진 지중열 추출량 조건에서 지중 열교환기의 총 길이를 산정하는 계산식을 제시하고 있다. 냉방 운전조건에 지중열 추출량에 따른 지중 열교환기 길이 산정식은 다음 식 (1)과 같다.
| $$L_c=\frac{q_aR_{ga}+(q_{lc}-W_c)(R_b+PLF_mR_{gm}+R_{gd}F_{sc})}{T_g-\frac{T_{wi}+T_{wo}}2-T_p}$$ | (1) |
여기서, Lc는 필요 지중 열교환기 길이 (m), qa는 연평균 지중열 추출량 (W), qc는 건물 냉방 부하(building design cooling block load) (W), Wc는 건물 냉방 부하조건에서 시스템 파워 (W), Rb는 지중 열교환기 열저항 (m·k/W), Rgm은 월평균 지중 부하에 기반한 유효 지중 열저항 (m·k/W), Rgd는 피크 지중 부하에 기반한 유효 지중 열저항 (m·k/W), PLFm은 월단위 부분 부하 계수(part-load factor during design month), Fsc는 쇼트 서킷 열손실 계수, Tg는 초기 지중 온도 (°C), Twi는 히트 펌프 열매체 유입 온도 (°C), Two는 히트 펌프 열매체 유출 온도 (°C), Tp는 페널티 온도 (°C)다.
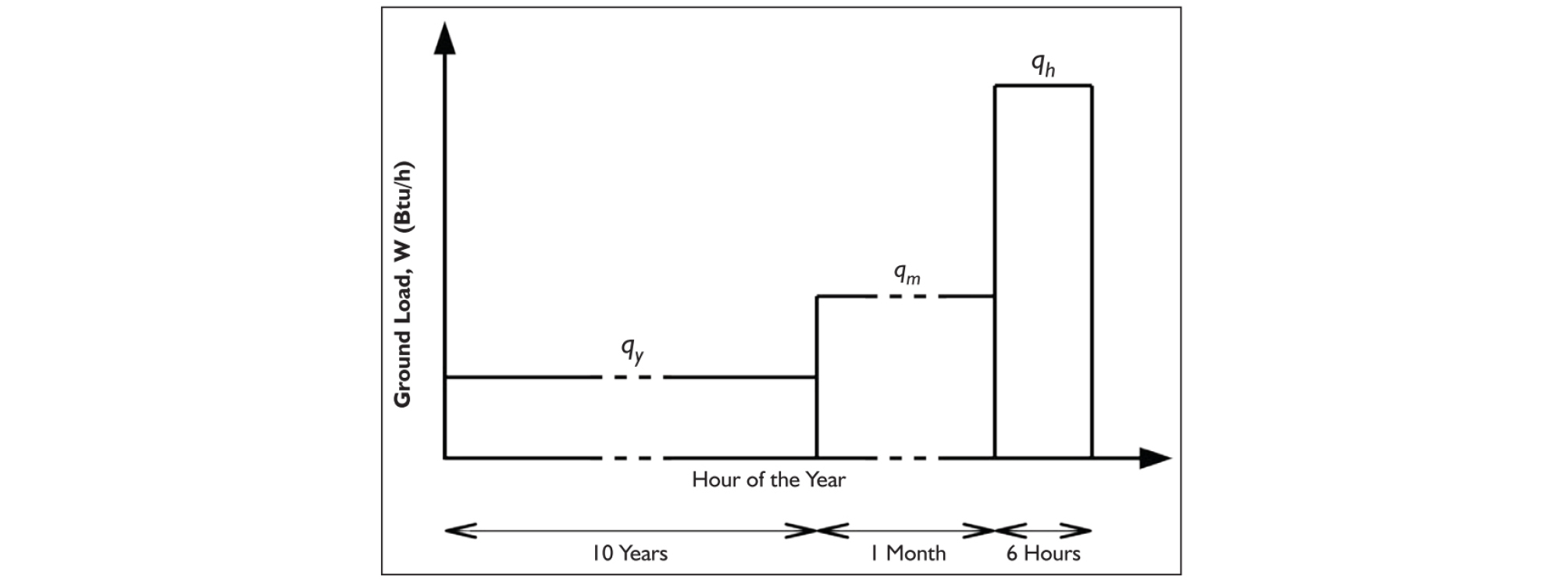
식 (1)에서는 시간에 따른 건물 냉방 부하를 블록 형태로 가정하여 계산에 활용한다. 즉, 매순간 변화하는 실제 냉방 부하를 아래 Figure 1과 같이 10년, 월, 피크 시간 동안 일정한 열류의 형태로 간략화하여 설계에 이용한다.
Design tool
실무에서는 GLHEpro, EED, GLD로 대표되는 지중 열교환기 디자인 툴이 일반적으로 사용되고 있다. 이러한 디자인 툴 역시 주어진 지중열 추출량 조건에서 지중 열교환기의 길이를 산정하는 방법이다. 건물 냉방부하와 지열 히트펌프의 성능 데이터에 기반해 산정된 지중열 추출량 데이터를 월 단위 또는 시간 단위의 열류로 가정하고 이를 지중 온도 변화 산정에 활용한다. 지중 온도 변화를 계산하기 위해 디자인 툴에서는 ASHRAE design procedure와 달리 다양한 지중 열교환기 배치에 대해서도 평가 가능한 g-function을 적용하였다.
ASHRAE deisgn procedure와 design tool 모두 실제 지열 히트펌프의 운영에 따른 지중열 추출량 변화를 시간, 월 또는 년 단위의 평균 열류의 형태로 가정한 뒤 일정한 열류가 연속적으로 지중으로 전달된다는 가정에서 지중 온도 변화를 산정한다. 즉, 비연속 운전 조건에서 지중열의 추출이 간헐적으로 이루어진다고 하더라도, 이를 연속적인 추출의 형태로 가정하게 되는 것이다. 따라서, 기존의 설계 방법에서는 지열 히트펌프의 비연속 운전 조건을 모델링하기 어렵고, 이는 히트 펌프의 운전이 중지 되는 동안에 지중에서 발생하는 지중 복원력 효과를 반영하는 것도 어렵다는 것을 의미한다. 기존 지중 열교환기 설계 방법에 대한 분석을 통해 지중 복원력을 고려한 설계를 수행하기 위해서는 새로운 설계 방법이 요구된다는 결론을 내릴 수 있다.
기존 지중 열교환기 열해석 모델
해석적 모델
지중 복원력을 고려한 지중 열교환기 설계 역시 지중열 추출에 따른 지중 온도의 산정이 요구된다. 우선, 해석적 모델은 지중 열교환기를 무한한 선형 또는 원통형의 heat source로 가정하고, 지중 열교환기에서 일정한 열류가 지중으로 전달되는 조건에서 지중 온도를 계산하는 방법이다. 해석적 모델의 대표적 모델인 무한 선형 열원 모델(Infinite Line Source model)은 아래 식 (2)와 같이 시간과 지중 열교환기에서 떨어진 거리에 따라서 지중 온도를 산정할 수 있도록 계산식이 구성되어 있다.
| $$T(r,t)-T_{t0}=\frac q{4\pi k}\int_\frac{r^2}{4\alpha t}^\infty\frac{e^{-u}}udu$$ | (2) |
여기서, T (r,t)는 지중 온도 (°C), r는 지중 열교환기로부터 떨어진 거리 (m), t는 시간 (s), Tto는 초기 지중 온도 (°C), q는 지중열 추출량 (W), k는 지중 열전도율 (W/m·K), α는 지중 열확산율 (m2/s)이다.
무한 선형 열원 모델에서는 지중 열교환기를 기준으로 수평 방향으로의 열류 이동만 고려하고 수직 방향으로의 열류 이동을 고려할 수 없다. 이는 지표면에서 일사열의 흡수, 지표면에서 대기와의 열전달로 인한 지중으로의 열획득/열손실을 반영할 수 없다는 것을 의미한다. 지표면에서의 열전달량은 지중 열교환기에서 지중으로 전달되는 열류량에 비해 그 양이 상대적으로 작은 편이지만, 장기간 운전 시 지표면 열전달량이 축적되어 지표면 열전달을 고려하지 않는 경우와 지중 온도 해석 결과의 차이가 크게 발생한다. 이를 보완하기 위한 목적으로 지중 열교환기를 유한한 선형의 열원으로 가정하는 유한 선형 열원 모델(Finite Line Source model) 또한 제안되었다.
응답함수 모델
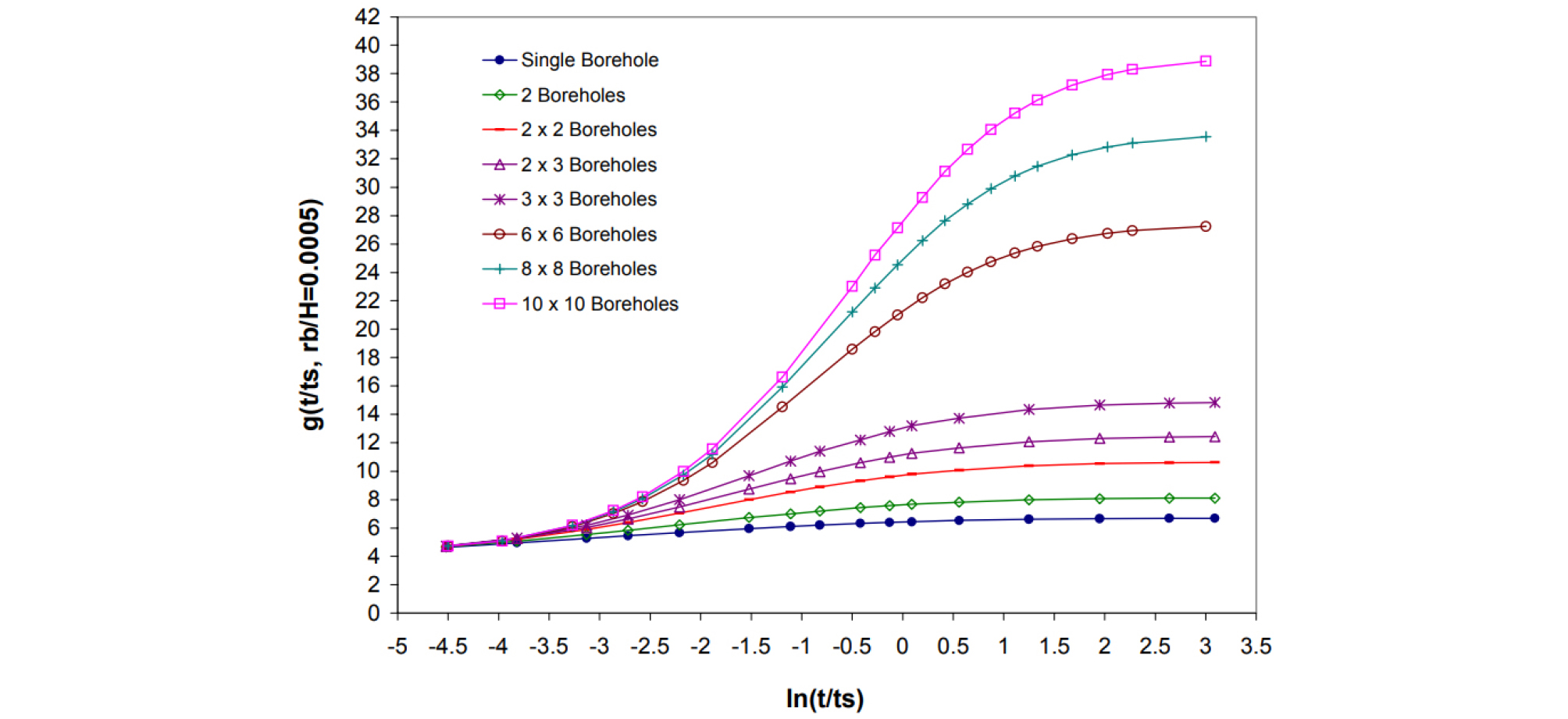
해석적 모델은 단일의 지중 열교환기를 대상으로 하기 때문에, 복수의 보어홀로 구성되는 멀티형 지중 열교환기가 설치된 지중의 온도 해석을 하기 위해서는 별도의 공간 중첩이론(spatial superposition)을 적용해야 한다. g-function으로 대표되는 응답함수 모델은 이러한 번거로움을 덜기 위해 지중 열교환기의 다양한 배치에 따른 성능 데이터세트를 Figure 2와 같이 제시하여 지중 온도 해석에 사용하도록 하고 있다. 이를 위해 Eskilson (1987)은 유한 차분법에 기반한 지중 열교환기 동적 열해석 프로그램을 개발하고, 프로그램을 이용하여 다양한 지중 열교환기의 배치에 따른 성능 데이터 세트를 생성하였다. 데이터세트는 아래 그림과 같이 배치 형태에 따라서 시간에 따른 응답 함수 계수를 확인할 수 있도록 구성되어 있다. g-function은 GLHEpro, EED, GLD와 같은 지중 열교환기 디자인 툴 뿐만 아니라 건물 에너지 동적 해석 프로그램인 EnergyPlus에도 적용되어 있다.
g-function 또한 지중 열교환기를 heat source로 가정하고 heat source에서 시간 단위 동안 일정한 열류가 연속적으로 지중으로 전달되는 조건에서 지중 온도를 해석하는 방법이다. 최근에는 응답 함수 생성시 지중 열교환기 경계 조건에 따른 영향을 분석한 연구들도 수행되고 있다.
수치해석 모델
해석적 모델과 응답함수 모델 모두 지중 열교환기에서 연속적인 지중열 추출을 가정하는 것을 확인하였다. Shirazi and Bernier (2013)의 연구에 따르면 지중열을 연속적으로 추출할때는 지중 열교환기의 축열 해석 여부가 성능 해석에 큰 영향을 미치지 않지만, 비연속 운전 조건에서는 축열 해석 여부에 따라서 성능 해석 결과 사이에 큰 차이가 발생한다. 따라서 해석적 모델과 응답함수 모델로는 비연속 운전 조건의 모델링과 지중열 복원에 대한 반영이 어렵다고 판단된다.
수치해석 모델은 지중 열교환기와 지중을 가장 상세하게 해석할 수 있는 방법이다. Marcotte and Pasquier (2008)의 연구에서는 3차원 유한요소 기법에 기반한 수치해석 모델을 제안하였고 이를 보어홀 열저항 산정의 정확도를 높히는데 활용하였다. He et al. (2009)의 연구에서는 보어홀 내부에서의 열적 거동을 짧은 시간 간격 단위에서도 분석하기 위한 목적으로 3차원 유한체적 기법에 기반한 수치해석 모델을 제안하였다. 기존의 수치해석에 기반한 모델에서는 지중 열교환기 내부와 외부 영역에 대해서 수많은 mesh를 생성한 뒤 유한 차분법, 유한 요소법 또는 유한 체적법을 적용하여 각 노드의 온도를 해석한다. 3차원 열전달 해석뿐만 아니라 축열 해석까지 가능하므로 지중 열교환기에서 발생하는 실제 열전달 현상을 대부분 반영할 수 있다. 즉 지중 열교환기로 공급되는 열매체 온도와 유량의 동적 변화까지 반영할 수 있으므로 실제 지열 히트펌프의 운전에 따른 지중 온도 변화를 평가할 수 있을 뿐만 아니라 지중 복원력에 대한 평가까지 가능하다.
하지만, 지중 열교환기와 지중 영역을 매우 세밀한 mesh로 분할하여 해석하는 정밀 수치해석 모델은 지중 복원력을 고려한 지중 열교환기 설계에 적합하지 않다. 단일한 지중 열교환기와 주변 지중의 mesh를 생성하면 수십만 개의 노드가 생성되고, 모든 노드에 대해서 10년 이상의 장기간의 온도 변화를 평가하는데 소요되는 시간을 고려한다면 설계 지원의 목적에서 정밀 수치해석 모델을 활용하는 것은 불가능하다고 판단된다.
이러한 어려움으로 인하여 기존 연구에서는 간략화된 수치해석 모델을 제안하여 지중 열교환기의 열성능 평가에 활용하고 있다. 대표적인 모델로 TRNSYS에 적용된 DST (Duct storage) 모델을 들 수 있다. DST의 경우 지중 열교환기 내부의 축열은 무시하고 외부의 지중 공간에 대해서 축열을 반영하고 있으며 유한 차분법을 적용하여 온도 해석을 하고 있다. 지중 열교환기 배치 또한 일정한 배열 형태로 가정하고 열교환기의 개수와 열교환기 사이의 거리에 따른 평가를 수행하여 해석의 간소화를 가능하게 하였다.
지중 열교환기 등가 열해석 모델 제안
지중 열교환기 등가 열해석 모델 주요 알고리즘
수치해석 모델은 지중 복원력을 고려한 지중 열교환기 설계의 보조적인 도구로써 사용되므로, 기존의 정밀 수치해석 모델과 같이 지중 열교환기 내외부를 매우 조밀한 mesh를 생성하여 해석하는 접근법은 해석 모델의 활용성 측면에서 적합하지 않다. 따라서 본 연구에서는 해석 모델의 활용도 측면에서 간략화된 지중 열교환기 열해석 모델을 제안하고자 한다.
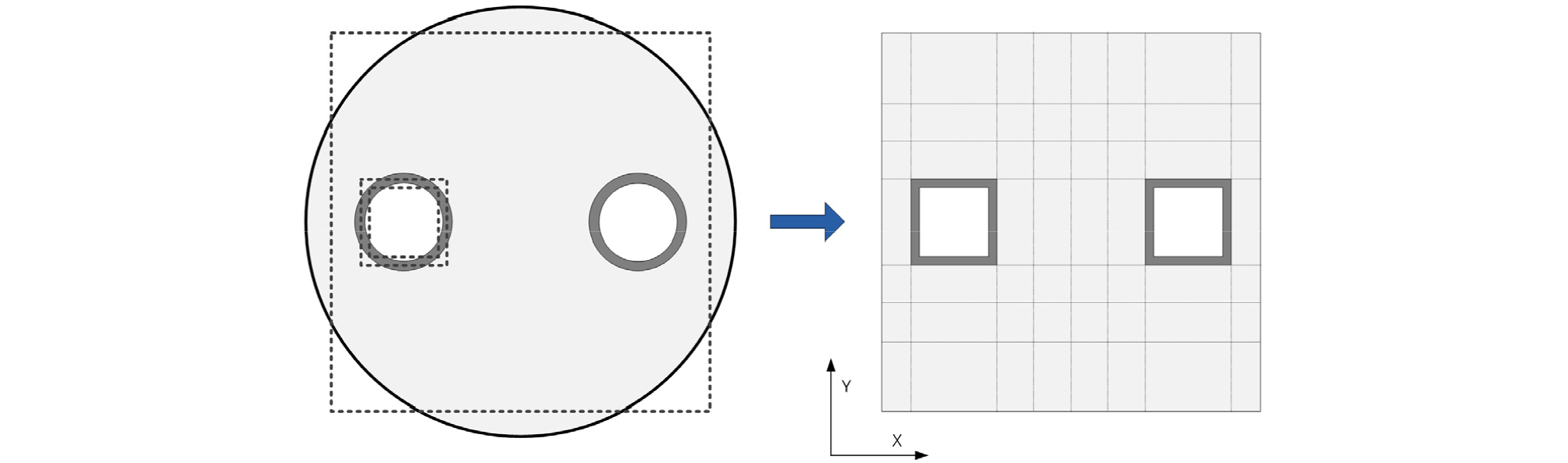
우선적으로 지중 열교환기와 지중 열교환기 주변의 지중 영역에 대해서 3차원 직교 좌표계를 적용하고 직육면체 형태의 mesh를 생성하였다. 하지만 지중 열교환기와 지중 열교환기 내부 배관의 단면 형상은 원형이므로 직교 좌표계를 적용하는데 어려움이 존재한다. 이를 해결하기 위해 배관과 지중 열교환기의 원형의 단면 형상을 정육면체의 단면 형상으로 변환하는 등가 모델을 제안하였다. Figure 3과 같이 단면 형상이 변하였다고 하더라도 열매체와 배관, 배관과 그라우트 재료, 그라우트 재료와 지중이 접촉하는 면적은 변환 전과 동일하게 설정하였고, 각 재료의 체적 또한 변환전과 변환후가 동일하게 설정하였다. 또한 열매체의 경우 평면상에서 각각 하나의 제어 체적으로 가정하였고, 그라우트 재료에 대해서는 다수의 제어 체적으로 분할하여 그라우트 재료의 온도 분포 또한 확인할 수 있도록 하였다. 지중 영역의 mesh 생성은 지중 열교환기 단면의 한 변의 길이를 기준으로 하였고, 지중 열교환기에서 멀어질수록 성글게 영역을 분할하였다. mesh 생성 후 각 노드에 대해서 열확산 방정식을 수립하고, 각 노드의 온도 해석을 수행하였다.
본 연구의 해석 모델에는 3차원 기반의 유한차분법이 적용되었으며, 각 노드에 대한 열확산 방정식은 다음 식 (3)-(5)과 같다. 식 (3)은 지중 방향의 배관 내 열매체에 대한 열확산 방정식으로 열매체에 대한 축열항과 주변 노드와 열매체 간의 열전달량을 계산하기 위한 항, 상하부 열매체 간의 순환에 따른 열전달량 계산의 항으로 구성된다. 식 (4)는 지표면 방향으로의 배관 내 열매체에 대한 열확산 방정식이며 식 (5)은 그라우트, 지중 노드에 대한 열확산 방정식이다. 식 (3)-(5) 모두 Gauss-Seidel에 기반한 수치해석 기법으로 모든 노드의 온도를 계산하였다.
여기서, ρ는 해당 재료의 밀도, cp는 해당 재료의 비열, Δx는 해당 노드의 x축 방향으로의 폭, Δy는 해당 노드의 y축 방향으로의 폭, Δz는 해당 노드의 z축 방향으로의 폭, Δt는 계산 시간간격, Ti,jkp+1는 해당 노드의 미래 시점의 온도, Ti,j,kp는 해당 노드의 현재 시점의 온도, Ti-1,j,kp+1, Ti+1,j,kp+1, Ti,j-1,kp+1, Ti,j+1,kp+1, Ti,j,k-1p+1, Ti-1,j,k+1p+1는 인접 노드의 미래 시점의 온도, 그리고 Ri-1, Ri+1, Rj-1, Rj+1, Rk-1, Rk+1은 각각 해당 노드와 인접 노드 간의 열저항을 의미한다.
지중 열교환기 등가 열해석 모델 검증
제안된 지중 열교환기 열해석 모델의 검증을 위해 샌드박스 테스트 데이터를 이용하였다. 지중 열교환기를 건물에 설치하기에 앞서 의무적으로 현장 열응답 시험을 수행하므로, 현장 열응답 시험 데이터를 활용한 열해석 모델의 검증 또한 가능하다. 하지만 현장 열응답 시험은 연속적인 운전 조건에서 수행되고, 시뮬레이션 모델링에 필요한 각 재료의 물성치, 지중 온도등과 같은 데이터를 확보하기 어려운 측면 또한 존재한다.
샌드박스 테스트는 Beier et al. (2011)에 의해 제안된 방법으로, 실험실에서 지중 열교환기를 모사하여 비연속 운전 조건에서 성능을 측정한 시험 방법이다. 지중 열교환기와 주변 재료의 열전도율을 측정하여 재료의 정확한 물성치를 확인할 수 있게 하였고, 샌드박스의 온도 또한 측정하였다. 저자는 새로운 해석 모델 개발 시 검증에 활용할 수 있도록 테스트 데이터를 온라인을 통해 제공하고 있고, 본 연구에서는 이를 활용하여 검증을 수행하였다.
샌드 박스 테스트의 측정 조건은 다음 Table 1과 같다. 실험은 총 50시간 동안 수행되었고, 초기 9시간 동안 연속적으로 지중열을 추출하고, 2시간 동안 운전을 중지한 뒤 다시 연속적으로 지중열을 추출하도록 시험이 진행되었다.
Table 1. Parameters for sandbox test with constant heat input rate
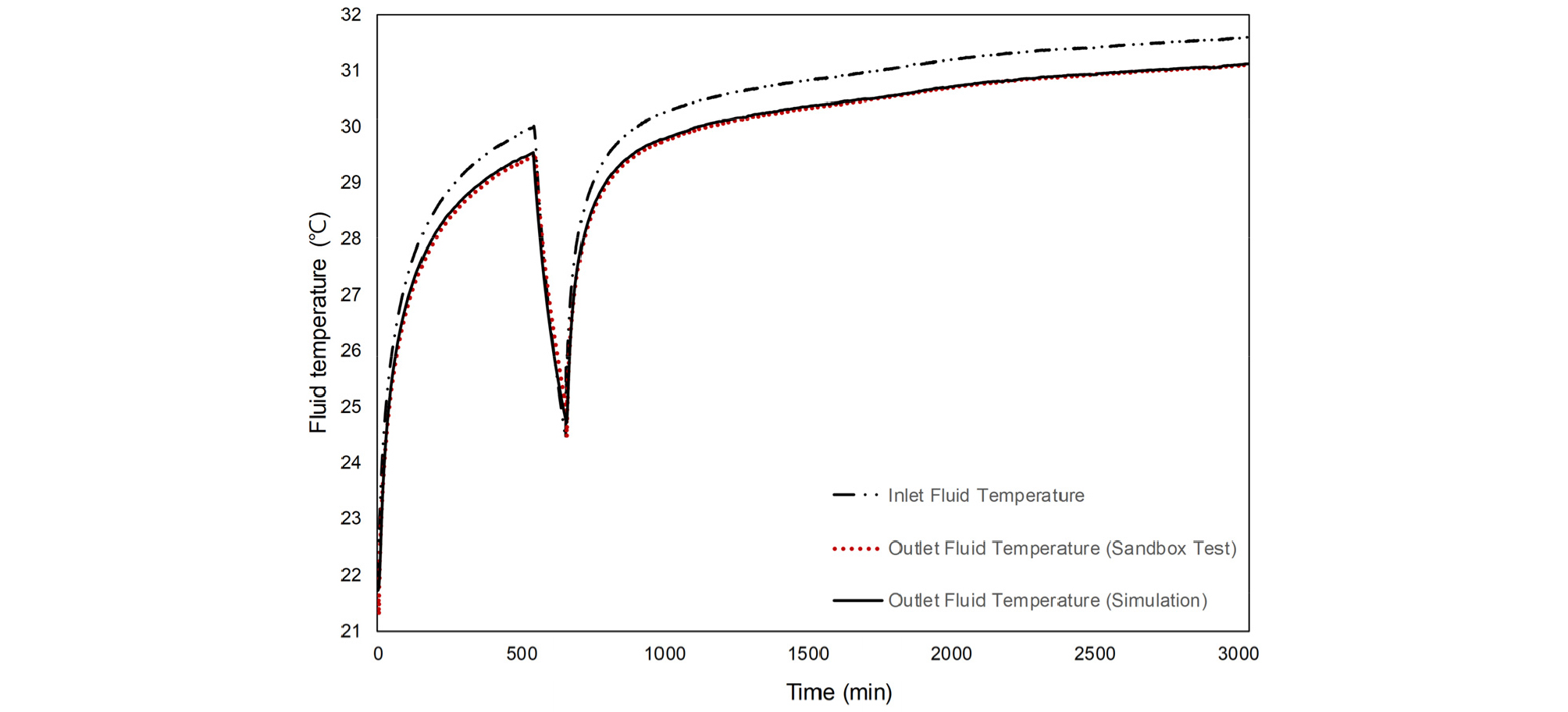
Table 1의 데이터를 참고하여 샌드 박스 테스트의 측정 조건과 동일한 조건을 열해석 모델에 모델링하여 시뮬레이션 결과를 얻었다. 열교환을 통해 얻어진 열매체의 환수 온도를 각각 비교한 결과는 아래 Figure 4와 같다. 열매체의 공급 온도 또한 Figure 4에 함께 표기하였다.
Figure 4에서 확인할 수 있듯이, 샌드박스 테스트에서 측정한 열매체의 환수 온도와 계산에 의해 얻어진 환수 온도의 결과가 거의 일치하는 것을 확인할 수 있다. 처음 9시간 동안의 샌드박스 테스트의 측정 결과와 시뮬레이션에 의한 계산 결과 사이의 평균 온도 차는 0.04°C이며, 운전이 중지되는 동안의 평균 온도차는 0.27°C, 다시 운전이 지속되는 동안의 온도차는 0.02°C이다. 운전 기간 동안에 두 결과는 거의 일치하는 것을 확인할 수 있으며 운전이 중지되는 동안에는 운전 기간에 비해 다소 오차가 큰 것을 확인할 수 있다. 이는 샌드박스 테스트 데이터에서 열용량과 관련된 재료의 비열, 밀도 데이터를 제시하지 않아 축열 해석에 있어 실제와 다소 차이가 있는 것으로 추정된다. 하지만 그 차이가 온도 센서의 오차 범위 안에 들만큼 작은 차이이므로 해석 모델의 정확도가 충분히 검증되었다고 볼 수 있다.
결 론
기존의 지중 열교환기 설계 방법에서는 연속적인 지중열 추출 조건을 가정하여 지중 온도 변화를 산정하고 이를 설계에 활용하고 있다. 하지만 최근의 연구에 따르면, 비연속 운전 조건에서 발생하는 지중 복원력으로 인하여 지중 열교환기 및 지열 히트펌프의 성능 향상과 경제적인 지중 열교환기의 설계가 가능함을 확인할 수 있다. 본 연구에서는 기존 지중 열교환기 설계 방법과 열해석 모델의 분석을 통해 지중 복원력을 반영한 설계를 위해서는 새로운 설계 방법의 제안이 필요하다는 결론을 내렸다. 지중 열교환기 설계에서 가장 중요한 지중 온도의 해석에 있어서도 해석적 방법이나 응답함수 모델보다는 간략화된 수치해석 모델의 제안이 필요하다.
이를 위해 본 연구에서는 등가 모델에 기반한 지중 열교환기 동적 열해석 모델을 제안하였다. 제안한 모델의 검증을 위해 샌드박스 테스트 측정 결과와 모델에서 계산된 결과를 비교하였다. 그 결과 두 방법을 통해 얻은 열매체 환수 온도의 결과가 거의 일치하는 것을 확인할 수 있었다. 따라서 지중 복원력을 고려한 지중 열교환기 설계를 위해서 본 연구에서 제안한 동적 열해석 모델의 활용이 가능할 것이라 판단된다.